【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC交⊙O于点F. 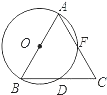
(1)AB与AC的大小有什么关系?为什么?
(2)按角的大小分类,请你判断△ABC属于哪一类三角形,并说明理由.
参考答案:
【答案】
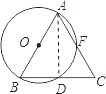
(1)解:连接AD.
∵AB是⊙O的直径,
∴AD⊥BC,
∵BD=CD,
∴AB=AC.
(2)解:连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠B<∠ADB=90度.
∠C<∠ADB=90度.
∴∠B、∠C为锐角.
∵AC和⊙O交于点F,连接BF,
∴∠A<∠BFC=90度.
∴△ABC为锐角三角形.
【解析】(1)连接AD,则AD垂直平分BC,那么AB=AC;(2)应把△ABC的各角进行分类,与直角进比较,进而求得△ABC的形状.
【考点精析】认真审题,首先需要了解等腰三角形的判定(如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等),还要掌握圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)x2+5x+7=3x+11
(2)x(2x﹣5)=4x﹣10. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
①画出△ABC关于x轴对称的△A1B1C1;
②画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2;
③△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴;
④△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.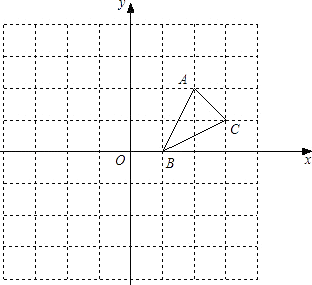
-
科目: 来源: 题型:
查看答案和解析>>【题目】多边形的内角和与某一个外角的度数和为1350度.
(1)求多边形的边数;
(2)此多边形必有一内角为多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线AB,CD,EF相交于点O,∠DOB的度数是它余角的2,∠AOE=2∠DOF,OG⊥AB.
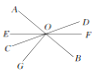
求:(1)∠DOB的度数;
(2)∠BOF的度数;
(3)∠EOG的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x+1)2﹣2的对称轴x=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中不正确的是( )
A. 两组对边分别平行的四边形是平行四边形
B. 对角线互相垂直的平行四边形是菱形
C. 有一个角是直角的平行四边形是矩形
D. 两条对角线互相垂直且相等的四边形是正方形
相关试题

