【题目】某中学举办“校园好声音”朗诵大赛,根据初赛成绩,七年级和八年级各选出5名选手组成七年级代表队和八年级代表队参加学校决赛两个队各选出的5名选手的决赛成绩如图所示:
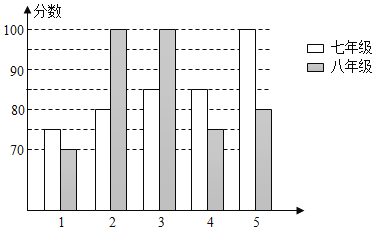
(1)根据所给信息填写表格;
平均数(分) | 中位数(分) | 众数(分) | |
七年级 | 85 | ||
八年级 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)若七年级代表队决赛成绩的方差为70,计算八年级代表队决赛成绩的方差,并判断哪个代表队的选手成绩较为稳定.
参考答案:
【答案】(1)填表见解析;(2)七年级代表队成绩好些;(3)七年级代表队选手成绩较为稳定.
【解析】
(1)根据平均数、众数和中位数的定义分别进行解答即可;
(2)根据表格中的数据,可以结合两个年级成绩的平均数和中位数,说明哪个队的决赛成绩较好;
(3)根据方差公式先求出八年级的方差,再根据方差的意义即可得出答案.
(1)八年级的平均成绩是:(75+80+85+85+100)÷5=85(分);
85出现了2次,出现的次数最多,则众数是85 分;
把八年级的成绩从小到大排列,则中位数是80分;
填表如下:
平均数(分) | 中位数(分) | 众数(分) | |
初二 | 85 | 85 | 85 |
初三 | 85 | 80 | 100 |
(2)七年级代表队成绩好些.
∵两个队的平均数都相同,七年级代表队中位数高,
∴七年级代表队成绩好些.
(3)S八年级2=![]() [(70-85)2+(100-85)2+(100-85)2+(75-85)2+(80-85)2]=160 ;
[(70-85)2+(100-85)2+(100-85)2+(75-85)2+(80-85)2]=160 ;
∵S七年级2<S八年级2,
∴七年级代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
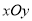 中,点
中,点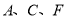 在坐标轴上,
在坐标轴上,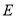 是
是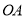 的中点,四边形
的中点,四边形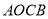 是矩形,四边形
是矩形,四边形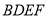 是正方形,若点
是正方形,若点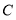 的坐标为
的坐标为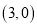 ,则点
,则点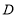 的坐标为( )
的坐标为( )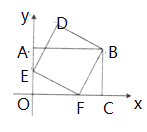
A.
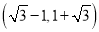 B.
B.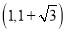 C.
C.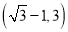 D.
D.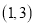
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与x轴交于A、B两点,与
与x轴交于A、B两点,与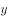 轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3.
轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3.
(1)求抛物线所对应的函数解析式.
(2)若点P为抛物线对称轴上的一个动点,求
 PAC周长的最小值.
PAC周长的最小值.(3)将AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.
-
科目: 来源: 题型:
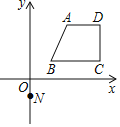
查看答案和解析>>【题目】如图,过点N(0,-1)的直线y=kx+b与图中的四边形ABCD有不少于两个交点,其中A(2,3)、B(1,1)、C(4,1)、D(4,3),则k的取值范围____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在∠MON的边ON上,AB⊥OM于B,AE=OB,DE⊥ON于E,AD=AO,DC⊥OM于C.
(1)求证:四边形ABCD是矩形;
(2)若DE=3,OE=9,求AB、AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某种产品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查发现,该产品每降价1元,每星期可多卖出20件,由于供货方的原因销量不得超过380件,设这种产品每件降价x元(x为整数),每星期的销售利润为w元.
(1)求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)该产品销售价定为每件多少元时,每星期的销售利润最大?最大利润是多少元?
(3)该产品销售价在什么范围时,每星期的销售利润不低于6000元,请直接写出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察猜想
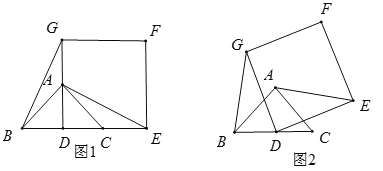
如图(1),在△ABC中,∠BAC=90°,AB=AC,点D是BC的中点.以点D为顶点作正方形DEFG,使点A,C分别在DG和DE上,连接AE,BG,则线段BG和AE的数量关系是_____;
(2)拓展探究
将正方形DEFG绕点D逆时针方向旋转一定角度后(旋转角度大于0°,小于或等于360°),如图2,则(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由.
(3)解决问题
若BC=DE=2,在(2)的旋转过程中,当AE为最大值时,直接写出AF的值.
相关试题

