【题目】将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边AC与含45°角的三角尺(△ACD)的斜边AC恰好重合.已知AB=2![]() ,P是AC上的一个动点.
,P是AC上的一个动点.
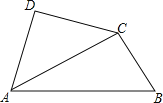
(1)当点P在∠ABC的平分线上时,求DP的长;
(2)当点PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D、P、B、Q为顶点构成平行四边形的顶点Q恰好在BC边上,求出此时DPBQ的面积.
参考答案:
【答案】(1)![]() .(2)15°或75°;(3)
.(2)15°或75°;(3)![]() .
.
【解析】
试题分析:(1)作DF⊥AC于F,由AB的长求得BC、AC的长.在等腰Rt△DAC中,DF=FA=FC;在Rt△BCP中,求得PC的长.则由勾股定理即可求得DP的长.
(2)由(1)得BC与DF的关系,则DP与DF的关系也已知,先求得∠PDF的度数,则∠PDA的度数也可求出,需注意有两种情况.
(3)由于四边形DPBQ为平行四边形,则BC∥DF,P为AC中点,作出平行四边形,求得面积.
解:在Rt△ABC中,AB=2![]() ,∠BAC=30°,
,∠BAC=30°,
∴BC=![]() ,AC=3.
,AC=3.
(1)如图(1),作DF⊥AC于F.
∵Rt△ACD中,AD=CD,
∴DF=AF=CF=![]() .
.
∵BP平分∠ABC,
∴∠PBC=30°,
∴CP=BCtan30°=1,
∴PF=![]() ,
,
∴DP=![]() =
=![]() .
.
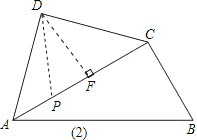
(2)当P点位置如图(2)所示时,
根据(1)中结论,DF=![]() ,∠ADF=45°,
,∠ADF=45°,
又∵PD=BC=![]() ,
,
∴cos∠PDF=![]() =
=![]() ,
,
∴∠PDF=30°.
∴∠PDA=∠ADF﹣∠PDF=15°.
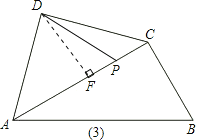
当P点位置如图(3)所示时,同(2)可得∠PDF=30°.
∴∠PDA=∠ADF+∠PDF=75°.
故∠PDA的度数为15°或75°;
(3)当点P运动到边AC中点(如图4),即CP=![]() 时,
时,
以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上.
∵四边形DPBQ为平行四边形,
∴BC∥DP,
∵∠ACB=90°,
∴∠DPC=90°,即DP⊥AC.
而在Rt△ABC中,AB=2![]() ,BC=
,BC=![]() ,
,
∴根据勾股定理得:AC=3,
∵△DAC为等腰直角三角形,
∴DP=CP=![]() AC=
AC=![]() ,
,
∵BC∥DP,
∴CP是平行四边形DPBQ的高,
∴S平行四边形DPBQ=DPCP=![]() .
.


-
科目: 来源: 题型:
查看答案和解析>>【题目】20140000用科学记数法表示(保留3个有效数字)为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋中装有除颜色外均相同的8个黑球、4个白球和若干个红球.每次摇匀后随机摸出一个球,记下颜色后再放回袋中,通过大量重复摸球试验后,发现摸到红球的频率稳定于0.4,由此可估计袋中约有红球个。
-
科目: 来源: 题型:
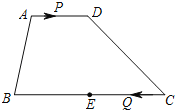
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,AD=4,BC=12,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间为 秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学用一副扑克牌中牌面数字分别是:3,4,5,6的4张牌做抽数学游戏.游戏规则是:将这4张牌的正面全部朝下,洗匀,从中随机抽取一张,抽得的数作为十位上的数字,然后,将所抽的牌放回,正面全部朝下、洗匀,再从中随机抽取一张,抽得的数作为个位上的数字,这样就得到一个两位数.若这个两位数小于45,则甲获胜,否则乙获胜.你认为这个游戏公平吗?请运用概率知识说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】木匠师傅锯木料时,一般先在木板上画出两个点,然后过这两点弹出一条墨线,这是因为( )
A.两点之间,线段最短
B.两点确定一条直线
C.两点之间线段的长度,叫做这两点之间的距离
D.圆上任意两点间的部分叫做圆弧 -
科目: 来源: 题型:
查看答案和解析>>【题目】某区10名学生参加市级汉字听写大赛,他们得分情况如下表:
人数
3
4
2
1
分数
80
85
90
95
那么这10名学生所得分数的平均数和众数分别是( ).
A.85和82.5 B.85.5和85 C.85和85 D.85.5和80
相关试题

