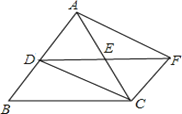
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,F是DE延长线上的点,且EF=DE.
(1)图中的平行四边形有哪几个?请说明理由;
(2)若△AEF的面积是3,求四边形BCFD的面积.
参考答案:
【答案】(1)图中的平行四边形有:平行四边形ADCF,平行四边形BDFC,理由见解析;
(2)平行四边形BCFD的面积为12.
【解析】试题分析:(1)由E为AC的中点,可得AE=CE,再由条件EF=DE可得四边形ADCF是平行四边形;(2)根据等底等高的三角形面积相等可得平行四边形对角线分成的四个小三角形面积相等可得△CEF的面积和△CED的面积都等于△AEF的面积为3,从而可得四边形BCFD的面积为12.
试题解析:(1)图中的平行四边形有:平行四边形ADCF,平行四边形BDFC,
理由是:∵E为AC的中点,
∴AE=CE,
∵DE=EF,
∴四边形ADCF是平行四边形,
∴AD∥CF,AD=CF,
∵D为AB的中点,
∴AD=BD,
∴BD=CF,BD∥CF,
∴四边形BDFC是平行四边形.
(2)由(1)知四边形ADCF是平行四边形,四边形BDFC是平行四边形,
∴S△CEF=S△CED=S△AEF=3,
∴平行四边形BCFD的面积是12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】双二次方程x4﹣2019x2+4=0的所有实根之和为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】教学楼里的大型多功能厅建成阶梯形状是为了( )
A. 美观 B. 宽敞明亮 C. 减小盲区 D. 容纳量大
-
科目: 来源: 题型:
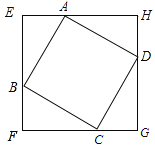
查看答案和解析>>【题目】如图,正方形ABCD的边长为8cm,分别过四个顶点A、B、C、D做四条直线EF、FG、GH、HE,并保证相邻两条直线垂直,相交于E、F、G、H四点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是正方形;
(2)判断无论如何按照上述要求作图,线段EG、AC的中点是否重合,并说明理由;
(3)判断四边形EFGH的面积有无最大值,若有请写出面积最大值,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程2x2﹣3x=1的根的情况是( )
A. 有两个不相等的实数根 B. 无实数根
C. 有两个相等的实数根 D. 无法判断
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016广东省茂名市第24题)如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=
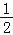 ∠A.
∠A.(1)求证:BC是⊙O的切线;
(2)若sinB=
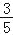 ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).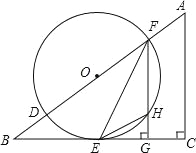
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察:从2开始,连续的偶数相加,它们的和的情况如下图:
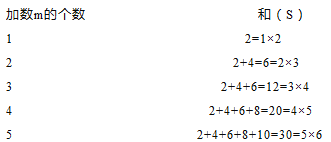
(1)和S与加数的个数m之间的数量关系为S= (用含m 的代数式表示);
(2)按此规律计算(写出必要的演算过程):
(i)2+4+6+┈+300 的值;
(ii)162+164+166+┈+400 的值.
相关试题

