【题目】如图,点P在![]() 的BC边上,利用直尺和三角板画出图形.
的BC边上,利用直尺和三角板画出图形.
(1)过点P作直线a与线段AB平行,交AC于点E;过点P作直线b与线段BC垂直,交AB于点F.
(2)在(1)的条件下,判断∠B与∠FPE的数量关系,请说明理由.

参考答案:
【答案】(1)见解析;(2) ∠B+∠FPE=90°,理由见解析.
【解析】
(1)根据平行和垂直的定义利用直尺和三角板画出图形即可;
(2)利用平行线和垂线的性质即可得出结论.
(1)如图,直线a与线段AB平行,交AC于点E; 直线b与线段BC垂直,交AB于点F;
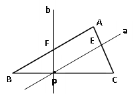
(2)证明:∵ PE∥AB
∴∠BFP =∠FPE
∵ FP⊥BC
∴∠B+∠BFP=90°
∴∠B+∠FPE=90°.
故答案为:(1)见解析;(2) ∠B+∠FPE=90°,理由见解析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0),C(2,2),将△ABC向左平移1个单位后再向下平移2单位,可得到△A′B′C′.
(1)请画出平移后的△A′B′C′的图形;
(2)写出△A′B′C′各个顶点的坐标;
(3)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中描出下列各点:A(3,0),B(-4,3),C(-4, -2),并解答:
(1)点A到原点O的距离是 个单位长度;
(2)将点B向下平移__________个单位,它会与点C重合;
(3)连接BC,直线BC与y轴的位置关系是__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共
 个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:
个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:摸球的次数





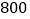


摸到白球的次数








摸到白球的频率








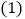 请估计:当实验次数为
请估计:当实验次数为 次时,摸到白球的频率将会接近________;(精确到
次时,摸到白球的频率将会接近________;(精确到 )
) 假如你摸一次,你摸到白球的概率
假如你摸一次,你摸到白球的概率 (摸到白球)
(摸到白球) ________;
________; 如何通过增加或减少这个不透明盒子内球的具体数量,使得在这个盒子里每次摸到白球的概率为
如何通过增加或减少这个不透明盒子内球的具体数量,使得在这个盒子里每次摸到白球的概率为 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,AB=CD,点E、F在BC上,且BE=CF.
(1)求证:△ABE≌△DCF;
(2)试证明:以A、F、D、E为顶点的四边形是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 在□ABCD中,点E、F是AD、BC的中点,连接BE、DF.
(1)求证:BE=DF.
(2)若BE平分∠ABC且交边AD于点E,AB=6cm,BC=10cm,试求线段DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.

解:∵EF∥AD(已知)
∴∠2=_________( )
∵∠1=∠2(已知)
∴∠1=__________( )
∴DG∥BA ( )
又∵∠BAC=70°(已知)
∴∠AGD=_________°( )
相关试题

