【题目】如图,某校教学楼AB的后面有一办公楼CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高3米的影子CE;而当光线与地面的夹角是45°时,教学楼顶A在地面上的影子F与墙角C有30米的距离(B、F、C在一条直线上).现要在A、E之间挂一些彩旗,求A、E之间的距离.(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() ,精确到0.1m)
,精确到0.1m)

参考答案:
【答案】A、E之间的距离约为58.7m.
【解析】试题分析:首先构造直角三角形△AEM,利用tan22°=![]() ,求出AB;利用Rt△AME中,cos22°=
,求出AB;利用Rt△AME中,cos22°=![]() ,求出AE即可.
,求出AE即可.
试题解析:
过点E作EM⊥AB,垂足为M.
设AB为x.
Rt△ABF中,∠AFB=45°,
∴BF=AB=x,
∴BC=BF+FC=x+30,
在Rt△AEM中,∠AEM=22°,AM=AB﹣BM=AB﹣CE=x﹣3,
tan22°=![]() ,
,
则![]() ,
,
解得:x=25.
∴ME=BC=x+30=25+30=55.
在Rt△AME中,cos22°=![]() .
.
∴AE=![]() =55÷
=55÷![]() =55×
=55×![]() ≈58.7,
≈58.7,
即A、E之间的距离约为58.7m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4
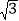 ,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将
,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将 绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为_____.
绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为_____.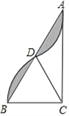
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=ax-b的图象经过一、二、三象限,且与x轴交于点(-2,0),则不等式ax>b的解集为
-
科目: 来源: 题型:
查看答案和解析>>【题目】坐标平面上有一点A,且A点到x轴的距离为3,A点到y轴的距离恰为到x轴距离的3倍,若A点在第二象限,则A点坐标为( )
A. (﹣3,9)B. (﹣3,1)C. (﹣9,3)D. (﹣1,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面生活中的物体的运动情况可以看成平移的是( )
A.随风摆动的旗帜B.摆动的钟摆
C.汽车玻璃上的雨刷的运动D.从楼顶自由下落的球(球不旋转)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
5台
1800元
第二周
4台
10台
3100元
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 等腰三角形底边上的中线就是底边的垂直平分线
B. 等腰三角形的对称轴是底边上的高
C. 一条线段可看做是以它的垂直平分线为对称轴的轴对称图形
D. 等腰三角形的对称轴就是顶角平分线
相关试题

