Question

【题目】在平面直角坐标系中，抛物线与轴交于点，，与轴交于点，直线经过，两点．

求抛物线的解析式；

在上方的抛物线上有一动点．

①如图，当点运动到某位置时，以，为邻边的平行四边形第四个顶点恰好也在抛物线上，求出此时点的坐标；

②如图，过点，的直线交于点，若，求的值．

Answer 1

【答案】．①点的坐标是；②．

【解析】

（1）由直线的解析式y=x+4易求点A和点C的坐标，把A和C的坐标分别代入y=-x2+bx+c求出b和c的值即可得到抛物线的解析式；
（2）①若以AP，AO为邻边的平行四边形的第四个顶点Q恰好也在抛物线上，则PQ∥AO，再根据抛物线的对称轴可求出点P的横坐标，由（1）中的抛物线解析式，进而可求出其纵坐标，问题得解；
②过P点作PF∥OC交AC于点F，因为PF∥OC，所以△PEF∽△OEC，由相似三角形的性质：对应边的比值相等可求出PF的长，进而可设点点F（x，x+4），利用(-x2-x+4)-(x+4)=，可求出x的值，解方程求出x的值可得点P的坐标，代入直线y=kx即可求出k的值．

∵直线经过，两点，

∴点坐标是，点坐标是，

又∵抛物线过，两点，

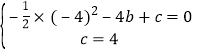∴，解得：，

∴抛物线的解析式为．①如图

∵，

∴抛物线的对称轴是直线．

∵以，为邻边的平行四边形的第四个顶点恰好也在抛物线上，

∴，．

∵，都在抛物线上，

∴，关于直线对称，

∴点的横坐标是，

∴当时，，

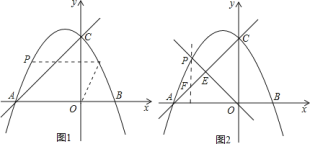
∴点的坐标是；

②过点作交于点，

∵，

∴，

∴．

又∵，

∴，

设点，

∴，

化简得：，解得：，．

当时，；当时，，

即点坐标是或．

又∵点在直线上，

∴．