搜索
【题目】在△ABC中BC=2，AB=2 
，AC=b，且关于x的方程x2﹣4x+b=0有两个相等的实数根，则AC边上的中线长为 ．
参考答案：
【答案】2
【解析】解：∵关于x的方程x2﹣4x+b=0有两个相等的实数根， ∴△=16﹣4b=0，
∴AC=b=4，
∵BC=2，AB=2 
，
∴BC2+AB2=AC2 ，
∴△ABC是直角三角形，AC是斜边，
∴AC边上的中线长= 
AC=2；
所以答案是：2．
【考点精析】本题主要考查了求根公式和直角三角形斜边上的中线的相关知识点，需要掌握根的判别式△=b2-4ac，这里可以分为3种情况：1、当△>0时，一元二次方程有2个不相等的实数根2、当△=0时，一元二次方程有2个相同的实数根3、当△<0时，一元二次方程没有实数根；直角三角形斜边上的中线等于斜边的一半才能正确解答此题．
-
科目： 来源： 题型：
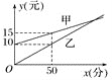
查看答案和解析>>【题目】如图所示，是某电信公司甲、乙两种业务：每月通话费用y(元)与通话时间x(分)之间的函数关系．某企业的周经理想从两种业务中选择一种，如果周经理每个月的通话时间都在100分钟以上，那么选择________种业务合算．
-
科目： 来源： 题型：
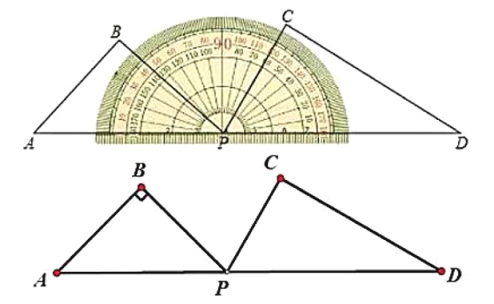
查看答案和解析>>【题目】一套三角尺（分别含
，，
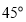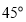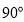和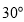
，
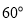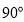，的角）按如图所示摆放在量角器上，边
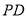与量角器
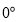刻度线重合，边
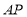与量角器
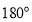刻度线重合，将三角尺
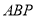绕量角器中心点
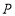以每秒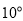
的速度顺时针旋转，当边
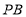与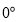刻度线重合时停止运动，设三角尺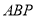的运动时间为
．
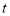（1）当
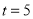时，边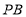经过的量角器刻度线对应的度数是 度；（2）若在三角尺
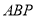开始旋转的同时，三角尺
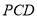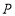也绕点以每秒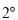
的速度逆时针旋转，当三角尺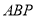停止旋转时，三角尺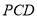也停止旋转．①当
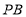为何值时，边平分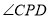
；②在旋转过程中，是否存在某一时刻使
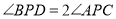，若存在，请求出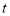的值；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中任意一点P(x0,y0)经平移后对应点为P′(x0＋3,y0＋4)，将△ABC作同样的平移得到△DEF，其中点A与点D，点B与点E，点C与点F分别对应，请解答下列问题：
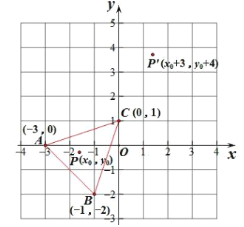
（1）直接写出点D、E、F的坐标；
（2）画出
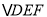，若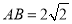
，
，
，
___________，
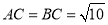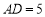______．（3）若将线段
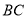沿某个方向进行平移得到线段MN，点 B(-1,-2)的对应点为 M ( m，0)，则点 C(0,1)的对应点 N 的坐标为________．（用含 m的式子表示） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，长青化工厂与A、B两地有公路、铁路相连．这家工厂从A地购买一批每吨2000元的原料运回工厂，制成每吨5000元的产品运到B地，已知公路运价为2元/（吨·千米），铁路运价为1.5元/（吨·千米），且这两次运输共支出公路运输费14000元，铁路运输费87000元．
（1）求：该工厂从A地购买了多少吨原料？制成运往B地的产品多少吨？
（2）这批产品的销售款比原料费与运输费的和多多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某运输公司用10辆相同的汽车将一批苹果运到外地，每辆汽车能装8吨甲种苹果，或10吨乙种苹果，或11吨丙种苹果．公司规定每辆车只能装同一种苹果，而且必须满载．已知公司运送了甲、乙、丙三种苹果共100吨，且每种苹果不少于一车．
（1）设用x辆车装甲种苹果，y辆车装乙种苹果，求y与x之间的函数关系式，并写出自变量x的取值范围；
（2）若运送三种苹果所获利润的情况如下表所示：
设此次运输的利润为W（万元），问：如何安排车辆分配方案才能使运输利润W最大，并求出最大利润．
-
科目： 来源： 题型：
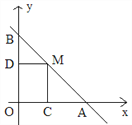
查看答案和解析>>【题目】如图，直线y=4－x与两坐标轴分别相交于A、B点，点M是线段AB上任意一点(A、B两点除外)，过M分别作MC⊥OA于点C，MD⊥OB于点D。
(1)当点M在AB上运动时，四边形OCMD的周长为________；
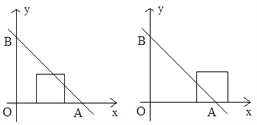
(2)当四边形OCMD为正方形时，将正方形OCMD沿着x轴的正方向移动，设平移的距离为a (0<a≤4)，在平移过程中：
①当平移距离a=1时, 正方形OCMD与△AOB重叠部分的面积为________；
②当平移距离a是多少时，正方形OCMD的面积被直线AB分成l：3两个部分?
相关试题
