【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
参考答案:
【答案】C
【解析】试题分析:①利用线段垂直平分线的性质的逆定理可得结论;②证△OMB≌△OEB得△EOB≌△CMB;
③先证△BEF是等边三角形得出BF=EF,再证DEBF得出DE=BF,所以得DE=EF;④由②可知△BCM≌△BEO,则面积相等,△AOE和△BEO属于等高的两个三角形,其面积比就等于两底的比,即S△AOE:S△BOE=AE:BE,由直角三角形30°角所对的直角边是斜边的一半得出BE=2OE=2AE,得出结论S△AOE:S△BOE=AE:BE=1:2.
①∵矩形ABCD中,O为AC中点, ∴OB=OC, ∵∠COB=60°, ∴△OBC是等边三角形, ∴OB=BC,
∵FO=FC, ∴FB垂直平分OC, 故①正确;
②∵FB垂直平分OC, ∴△CMB≌△OMB, ∵OA=OC,∠FOC=∠EOA,∠DCO=∠BAO, ∴△FOC≌△EOA,
∴FO=EO, 易得OB⊥EF, ∴△OMB≌△OEB, ∴△EOB≌△CMB, 故②正确;
③由△OMB≌△OEB≌△CMB得∠1=∠2=∠3=30°,BF=BE, ∴△BEF是等边三角形, ∴BF=EF,
∵DF∥BE且DF=BE, ∴四边形DEBF是平行四边形, ∴DE=BF, ∴DE=EF, 故③正确;
④在直角△BOE中∵∠3=30°, ∴BE=2OE, ∵∠OAE=∠AOE=30°, ∴AE=OE, ∴BE=2AE,
∴S△AOE:S△BCM=S△AOE:S△BOE=1:2, 故④错误;
所以其中正确结论的个数为3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )

A. 5 B. 8 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,点E在BA的延长线上,点D在BC边上,且ED=EC.若△ABC的边长为4,AE=2,则BD的长为( )

A.2
B.3
C.
D. +1
+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C﹣D﹣E上移动,若点C、D、E的坐标分别为(﹣1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )

A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】等边
 在数轴上的位置如图所示,点A、C对应的数分别为0和
在数轴上的位置如图所示,点A、C对应的数分别为0和 ,若
,若 绕顶点沿顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1,则连续翻转2012次后,点B( )
绕顶点沿顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1,则连续翻转2012次后,点B( )
A. 不对应任何数 B. 对应的数是2010
C. 对应的数是2011 D. 对应的数是2012
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为非零的实数,则
 的可能值的个数为( )
的可能值的个数为( )A. 4 B. 5 C. 6 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》
(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形式面积是1,直角三角形的短直角边为a,较长直角边为b,那么
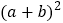 的值为________.
的值为________. 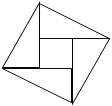
相关试题

