【题目】(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.
①填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示)
(2)应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB、AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.

参考答案:
【答案】(1)CB的延长线上,a+b;(2)①CD=BE.理由见解析;②线段BE长的最大值为4.理由见解析.
【解析】试题分析:(1)根据点A为线段BC外一动点,且BC=a,AB=b,可得当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b;
(2)①根据等边三角形ABD和等边三角形ACE,可得△CAD≌△EAB(SAS),根据全等三角形的性质可得CD=BE;
②根据全等三角形的性质可得,线段BE长的最大值=线段CD长的最大值,而当线段CD的长取得最大值时,点D在CB的延长线上,此时CD=3+1=4,可得BE=4.
试题解析:(1)如图1,
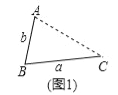
∵点A为线段BC外一动点,且BC=a,AB=b,
∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b.
(2)①CD=BE.
理由:如图2,
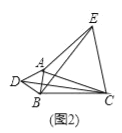
∵三角形ABD和三角形ACE是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠CAD=∠EAB,
在△CAD和△EAB中,
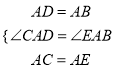
∴△CAD≌△EAB(SAS),
∴CD=BE;
②线段BE长的最大值为4.
理由:∵线段BE长的最大值=线段CD长的最大值,
∴当线段CD的长取得最大值时,点D在CB的延长线上,
此时CD=3+1=4,
∴BE=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.x2+x3=2x5B.x2 x3=x6C.(﹣x3)2=﹣x5D.x6÷x3=x3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列条件中,不能证明△ABD≌△ACD的是( )

A. BD=DC ,AB=AC B. ∠ADB=∠ADC,∠BAD=∠CAD
C. ∠B=∠C, BD=DC D. ∠B=∠C ,∠BAD=∠CAD
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P(x,y)的坐标满足xy=0(x≠y),则点P在( )
A. 原点上B. x轴上C. y轴上D. 坐标轴上
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列正确说法的是____
①同位角相等; ②等角的补角相等; ③两直线平行,同旁内角相等;④在同一平面内,过一点有且只有一条直线与已知直线垂直.
-
科目: 来源: 题型:
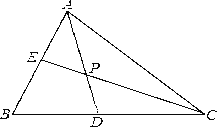
查看答案和解析>>【题目】如图,△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,AD、CE相交于点P
(1) 求∠CPD的度数
(2) 若AE=3,CD=7,求线段AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种细菌在培养过程中,每1小时分裂一次,每次一分为二,这种细菌由1个分裂到8个要经过( )
A.3小时B.4小时C.5小时D.6小时
相关试题

