【题目】如图,△ABC是一个等腰直角三角形,DEFG是其内接正方形,H是正方形的对角线交点;那么,由图中的线段所构成的三角形中相互全等的三角形的对数为( ) 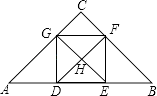
A.12
B.13
C.26
D.30
参考答案:
【答案】C
【解析】
解答:解:设AB=3,图中所有三角形均为等腰直角三角形,其中,斜边长为1的有5个,它们组成10对全等三角形;
斜边长为 ![]() 的有6个,它们组成15对全等三角形;
的有6个,它们组成15对全等三角形;
斜边长为2的有2个,它们组成1对全等三角形;
共计26对.
故选C
分析:根据全等三角形的判定可以确定全等三角形的对数,由于图中全等三角形的对数较多,可以根据斜边长的不同确定对数,可以做到不重不漏.本题考查了全等三角形的判定,涉及到等腰直角三角形和正方形的性质,解题的关键是记熟全等三角形的判定方法并做到不重不漏
【考点精析】根据题目的已知条件,利用等腰直角三角形和正方形的性质的相关知识可以得到问题的答案,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个n边形的内角和是它外角和的6倍,则n=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市今年的信息技术结业考试,采用学生抽签的方式决定自己的考试内容.规定:每位考生先在三个笔试题(题签分别用代码B1、B2、B3表示)中抽取一个,再在三个上机题(题签分别用代码J1、J2、J3表示)中抽取一个进行考试.小亮在看不到题签的情况下,分别从笔试题和上机题中随机地抽取一个题签.
(1)用树状图或列表法表示出所有可能的结果;
(2)求小亮抽到的笔试题和上机题的题签代码的下标(例如“B1”的下标为“1”)为一个奇数一个偶数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的四边形ABCD,并写出了如下不完整的已知和求证.已知:如图,在四边形ABCD中,BC=AD,
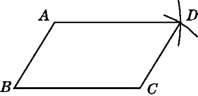
AB=__①___.
求证:四边形ABCD是___②___四边形.
(1)在方框中填空,以补全已知和求证;
①;②.
(2)按嘉淇的想法写出证明.
(3)用文字叙述所证命题的逆命题为 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
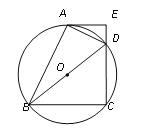
(1)求证:AE⊥CD;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x﹣2)x=1,则x=___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为减少环境污染,自2008年6月1日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分:
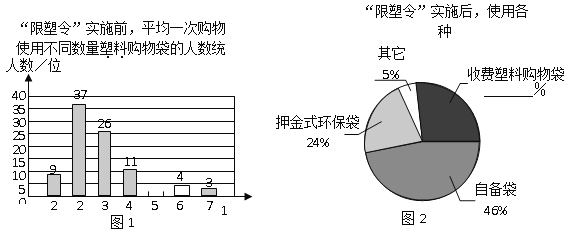
“限塑令”实施后,塑料购物袋使用后的处理方式统计表
处理方式
直接丢弃
直接做垃圾袋
再次购物使用
其它
选该项的人数占
总人数的百分比
5%
35%
49%
11%
请你根据以上信息解答下列问题:
(1)补全图1,“限塑令”实施前,如果每天约有2 000人次到该超市购物.根据这100位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市每天需要为顾客提供多少个塑料购物袋?
(2)补全图2,并根据统计图和统计表说明,购物时怎样选用购物袋,塑料购物袋使用后怎样处理,能对环境保护带来积极的影响.
相关试题

