Question

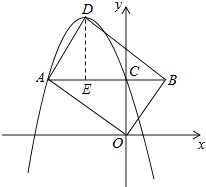
【题目】如图，已知在平面直角坐标系xOy中，O是坐标原点，抛物线y=﹣x2+bx+c（c＞0）的顶点为D，与y轴的交点为C，过点C作CA∥x轴交抛物线于点A，在AC延长线上取点B，使BC= AC，连接OA，OB，BD和AD．

（1）若点A的坐标是（﹣4，4）．
①求b，c的值；
②试判断四边形AOBD的形状，并说明理由；
（2）是否存在这样的点A，使得四边形AOBD是矩形？若存在，请直接写出一个符合条件的点A的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：①∵AC∥x轴，A点坐标为（﹣4，4）．

∴点C的坐标是（0，4）

把A、C两点的坐标代入y=﹣x2+bx+c得，

，

解得 ；

②四边形AOBD是平行四边形；

理由如下：

由①得抛物线的解析式为y=﹣x2﹣4x+4，

∴顶点D的坐标为（﹣2，8），

过D点作DE⊥AB于点E，

则DE=OC=4，AE=2，

∵AC=4，

∴BC= AC=2，

∴AE=BC．

∵AC∥x轴，

∴∠AED=∠BCO=90°，

∴△AED≌△BCO，

∴AD=BO．∠DAE=∠OBC，

∴AD∥BO，

∴四边形AOBD是平行四边形．

（2）

解：存在，点A的坐标可以是（﹣2 ，2）

要使四边形AOBD是矩形；

则需∠AOB=∠BCO=90°，

∵∠ABO=∠OBC，

∴△ABO∽△OBC，

∴ ，

又∵AB=AC+BC=3BC，

∴OB= BC，

∴在Rt△OBC中，根据勾股定理可得：OC= BC，AC= OC，

∵C点是抛物线与y轴交点，

∴OC=c，

∴A点坐标为（﹣ c，c），

∴顶点横坐标 =﹣ c，b=﹣ c，

顶点D纵坐标是点A纵坐标的2倍，为2c，

顶点D的坐标为（﹣ c，2c）

∵将D点代入可得2c=﹣（﹣ c）2+ c c+c，

解得：c=2或者0，

当c为0时四边形AOBD不是矩形，舍去，故c=2；

∴A点坐标为（﹣2 ，2）．

【解析】（1）①将抛物线上的点的坐标代入抛物线即可求出b、c的值；
②求证AD=BO和AD∥BO即可判定四边形为平行四边形；（2）根据矩形的各角为90°可以求得△ABO∽△OBC即 ，再根据勾股定理可得OC= BC，AC= OC，可求得横坐标为﹣ c，纵坐标为c．
【考点精析】关于本题考查的二次函数的性质，需要了解增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能得出正确答案．