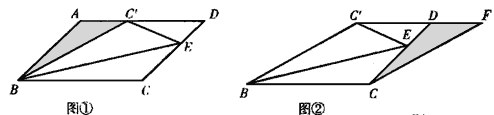
【题目】如图①,四边形ABCD为平行四边形,E在CD边上,将△BCE沿BE翻折,点C刚好落在AB边上的点C′处
(1)在图①中,请直接写出四对相等的线段;
(2)将图①中的△ABC′剪下并拼接在图②中△DCF的位置上(其中△ABC′的三个顶点A、B、C′分别与△DCF的三个顶点D、C、F重合,并且图②的点C′、D、F在同一直线上)试证明图②中的四边形BCFC′是菱形.
参考答案:
【答案】(1)、AB=CD,AD=BC,BC=BC′,EC=EC′;(2)、证明过程见解析
【解析】
试题分析:(1)、根据平行四边形的性质以及折叠图形的性质得出答案;(2)、根据平行四边形的性质得出BC=AD,BC∥C′D,根据图形得出△ABC′≌△DCF,然后根据线段之间的关系得出BC= C′F,从而得出四边形BCFC′为平行四边形,根据折叠图形的性质得出BC=BC′,从而得出菱形.
试题解析:(1)AB=CD,AD=BC,BC=BC′,EC=EC′
(2)、在图①中, ∵四边形ABCD为平行四边形,∴BC=AD,BC∥C′D
在图①与图②中,由题意知:△ABC′≌△DCF,
∴AC′=DF
∴AC′+C′D= C′D +DF
∴AD= C′F,即得BC= C′F
∵BC∥C′F,∴四边形BCFC′为平行四边形
又由折叠的性质得:BC=BC′,
∴四边形BCFC′为菱形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是最小的正整数,b的相反数还是它本身,c比最大的负整数大3,则(2a+3c)b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系内的点A(﹣1,2)与点B(﹣1,﹣2)关于( )
A.y轴对称 B.x轴对称 C.原点对称 D.直线y=x对称
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填空: 31—30=2×3( ), 32—31=2×3( ), 33—32=2×3( ) , …
(2)探索(1)中式子的规律,试写出第n个等式,并说明第n个等式成立;
(3)利用上述规律计算:30+31+32+33+…+32015+32016= ,
其末位数字是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,M 是AB的中点,且AN=
 AD,问△CMN是什么三角形?并加以证明。
AD,问△CMN是什么三角形?并加以证明。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠长方形的一边AD,使点D 落在BC边上的点F处, BC=15cm,AB=9cm
求(1)FC的长;(2)EF的长.

-
科目: 来源: 题型:
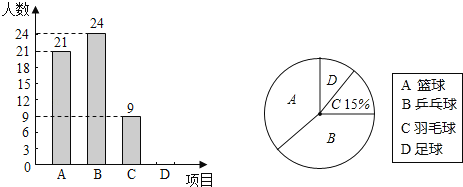
查看答案和解析>>【题目】某校为了解该校九年级学生对蓝球、乒乓球、羽毛球、足球四种球类运动项目的喜爱情况,对九年级部分学生进行了随机抽样调查,每名学生必须且只能选择最喜爱的一项运动项目,将调查结果统计后绘制成如图两幅不完整的统计图,请根据图中的信息,回答下列问题:
(1)这次被抽查的学生有 人;请补全条形统计图;
(2)在统计图2中,“乒乓球”对应扇形的圆心角是 度;
(3)若该校九年级共有480名学生,估计该校九年级最喜欢足球的学生约有 人.
相关试题

