【题目】计算
(1)![]()
(2)(﹣a)2a4÷a3
(3)(2x﹣1)(x﹣3)
(4)(3x﹣2y)2(3x+2y)2
(5)(x﹣2y+4)(x﹣2y﹣4)
参考答案:
【答案】解:(1)![]()
=﹣4﹣2+1
=﹣5;
(2)(﹣a)2a4÷a3
=a2a4÷a3
=a3;
(3)(2x﹣1)(x﹣3)
=2x2﹣6x﹣x+3
=2x2﹣7x+3;
(4)(3x﹣2y)2(3x+2y)2
=[(3x﹣2y)(3x+2y)]2
=(9x2﹣4y2)2
=81x4﹣72x2y2+16y4
(5)(x﹣2y+4)(x﹣2y﹣4)
=(x﹣2y)2﹣42
=x2﹣4xy+4y2﹣16
【解析】(1)根据有理数的乘方法则、负整数指数幂的定义和零指数幂的定义计算,再合并即可;
(2)根据同底数幂的乘除法法则计算即可;
(3)根据多项式与多项式相乘的法则计算,再合并即可;
(4)先运用平方差公式计算,再运用完全平方公式计算即可;
(5)先运用平方差公式计算,再运用完全平方公式计算即可.
【考点精析】解答此题的关键在于理解零指数幂法则的相关知识,掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数),以及对完全平方公式的理解,了解首平方又末平方,二倍首末在中央.和的平方加再加,先减后加差平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣|﹣2017|= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】课本拓展
旧知新意:
我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
1.尝试探究:
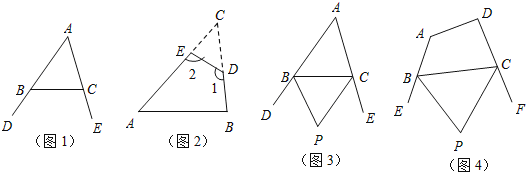
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
2.初步应用:
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=130°,则∠2-∠C= ;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案 .
3拓展提升:
(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明准备测量一段河水的深度,他把一根竹竿竖直插到离岸边1.5 m远的水底,竹竿高出水面0.5 m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
A. 3 m B. 2.5 m C. 2.25 m D. 2 m
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+2与x轴交于点A(1,0)和B(4,0).
(1)求抛物线的解析式及对称轴;
(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式3x2﹣x3+5x4﹣7+23x,将该多项式按降幂排列( )
A. 3x2﹣x3+5x4﹣7+23x B. 5x4+23x+3x2﹣x3﹣7
C. 5x4﹣x3+3x2+23x﹣7 D. ﹣x3+5x4+3x2﹣7+23x
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=
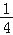 BD;
BD;其中正确结论的是( )

A.①②③ B.①②④ C.①③④ D.②③④
相关试题

