【题目】为了保护环境,某化工厂一期工程完成后购买了3台甲型和2台乙型污水处理设备,共花费资金54万元,且每台乙型设备的价格是每台甲型设备价格的75%,实际运行中发现,每台甲型设备每月能处理污水200吨,每台乙型设备每月能处理污水160吨,且每年用于每台甲型设备的各种维护费和电费为1万元,每年用于每台乙型设备的各种维护费和电费为1.5万元.今年该厂二期工程即将完成,产生的污水将大大增加,于是该厂决定再购买甲、乙两型设备共8台用于二期工程的污水处理,预算本次购买资金不超过84万元,预计二期工程完成后每月将产生不少于1300吨污水.
(1)请你计算每台甲型设备和每台乙型设备的价格各是多少元?
(2)请你求出用于二期工程的污水处理设备的所有购买方案;
(3)若两种设备的使用年限都为10年,请你说明在(2)的所有方案中,哪种购买方案的总费用最少?(总费用=设备购买费+各种维护费和电费)
参考答案:
【答案】(1)设一台甲型设备的价格为x万元,由题![]() ,解得x=12,∵ 12×75%=9 ,∴ 一台甲型设备的价格为12万元,一台乙型设备的价格是9万元
,解得x=12,∵ 12×75%=9 ,∴ 一台甲型设备的价格为12万元,一台乙型设备的价格是9万元
设二期工程中,购买甲型设备a台,
由题意有![]() ,解得:
,解得:![]()
由题意a为正整数,∴a=1,2,3,4 ∴所有购买方案有四种,分别为
方案一:甲型1台,乙型7台; 方案二:甲型2台,乙型6台
方案三:甲型3台,乙型5台; 方案四:甲型4台,乙型4台
(3)设二期工程10年用于治理污水的总费用为W万元
![]() 化简得:
化简得: ![]() -2a+192,
-2a+192,
∵W随a的增大而减少 ∴当a=4时, W最小(逐一验算也可)
∴按方案四甲型购买4台,乙型购买4台的总费用最少.
【解析】(1)由题中提炼出的1个等量关系,购买了3台甲型和2台乙型污水处理设备,共花费资金54万元,且每台乙型设备的价格是每台甲型设备价格的75%,即可列方程求出;
(2)根据题意列出不等方程组,再解出未知量的取值范围;
(3)首先根据已知得出W与x的函数关系,再利用一次函数的增减性进行分析的得出答案即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN=_____.
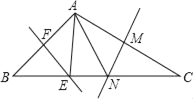
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,四边形OABC为菱形,A点的坐标为
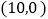 ,对角线OB、AC相交于D点,双曲线
,对角线OB、AC相交于D点,双曲线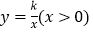 经过D点,交BC的延长线于E点,且
经过D点,交BC的延长线于E点,且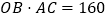 ,则E点的坐标是
,则E点的坐标是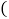

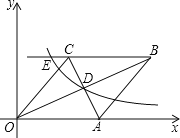
A.
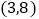 B.
B. 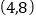 C.
C. 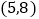 D.
D. 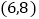
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
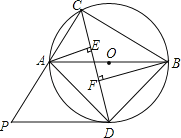
(1)求证:DP∥AB;
(2)若AC=6,BC=8,求线段PD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学在用描点法画二次函数
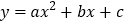 的图象时,列出下面的表格:
的图象时,列出下面的表格:x

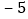
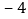
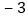
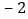
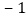

y

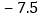
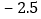
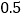
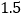
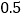

根据表格提供的信息,有下列结论:
 该抛物线的对称轴是直线
该抛物线的对称轴是直线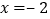 ;
;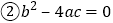 ;
; 该抛物线与y轴的交点坐标为
该抛物线与y轴的交点坐标为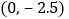 ;
; 若点
若点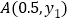 是该抛物线上一点,则
是该抛物线上一点,则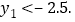 其中错误的个数是
其中错误的个数是

A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.

(1)求证:△ABG≌△C′DG;
(2)求tan∠ABG的值;
(3)求EF的长.
相关试题

