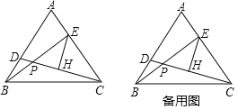
【题目】如图,在等边△ABC中,点D、点E分别在AB、AC上,BD=AE,连接BE、CD交于点P,作EH⊥CD于H.
(1)求证:△CAD≌△BCE;(2)求证:PE=2PH;(3)若PB=PH,求∠ACD的度数.
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)45°
【解析】
(1)根据SAS证明△CAD≌△BCE即可;
(2)利用直角三角形30度角的性质即可解决问题;
(3)连接AH、BH,过H点作HM⊥AB于M,HN⊥AC于N.利用全等三角形的性质证明△EHC是等腰直角三角形即可解决问题;
(1)证明:如图1中,

∵△ACB是等边三角形,
∴∠A=∠BCA=∠ABC=60°,AB=AC=BC,
∵BD=AE,
∴AB-BD=AC-AE,
即AD=EC,
在△CAD与△BCE中,
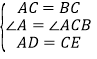 ,
,
∴△CAD≌△BCE(SAS).
(2)证明:如图2中,
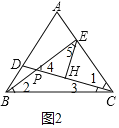
由(1)得△CAD≌△BCE,
∴∠1=∠2,
∵∠1+∠3=60°,
∴∠2+∠3=60°,
∴∠4=∠2+∠3=60°,
又∵EH⊥CD,
∴∠PHE=90°即△PHE是直角三角形,
∵∠5=90°-∠4=30°,
∴PH=![]() PE.
PE.
即PE=2PH.
(3)解:连接AH、BH,过H点作HM⊥AB于M,HN⊥AC于N.
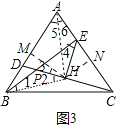
∵PB=PH,
∠1=∠2,
由(2)得,∠4=30°,
∠3=∠1+∠2=60°,
∴∠1=∠2=30°,
∴∠BHE=120°,
∴∠1=∠4,
∴BH=EH,
∵∠BAC=60°,
∴∠ABH+∠AEH=360°-∠BAC+∠BHE=180°,
∵∠HEC+∠AEH=180°,
∠ABH=∠HEC,
∴∠BMH=∠ENH=90°,
∴△BHM≌△EHN(AAS),
∴HM=HN,
∴∠5=∠6,
∵AH=AH,AB=AC,
∴△AHB≌△AHC(SAS0,
∴HB=HC=HE且∠EHC=90°.
∴∠ACD=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O在AB上,⊙O与AB交于点E.

(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径. -
科目: 来源: 题型:
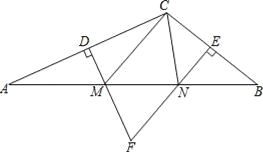
查看答案和解析>>【题目】如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)若△CMN的周长为15cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.
-
科目: 来源: 题型:
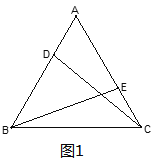
查看答案和解析>>【题目】在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以每分钟1米的速度由A向B和由C向A爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t分钟后,它们分别爬行到D、E处,请问:
(1)如图1,在爬行过程中,CD和BE始终相等吗,请证明?
(2)如果将原题中的“由A向B和由C向A爬行”,改为“沿着AB和CA的延长线爬行”,EB与CD交于点Q,其他条件不变,蜗牛爬行过程中∠CQE的大小保持不变,请利用图2说明:∠CQE=60°;
(3)如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行,连接DE交AC于F”,其他条件不变,如图3,则爬行过程中,证明:DF=EF



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠5=∠6,∠3=∠4,试说明AE∥BD,AD∥BC.请完成下列证明过程.
证明:
∵∠5=∠6,
∴AB∥CE( ),
∴∠3=__________
∵∠3=∠4,
∴∠4=∠BDC( ),
∴ ∥BD( ),
∴∠2= ( )
∵∠1=∠2,
∴∠1=______,
∴AD∥BC

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标平面内,直线y=-x+5与
 轴和
轴和  轴分别交于A、B两点,二次函数y=
轴分别交于A、B两点,二次函数y=  +bx+c的图象经过点A、B,且顶点为C.
+bx+c的图象经过点A、B,且顶点为C.
(1)求这个二次函数的解析式;
(2)求sin∠OCA的值;
(3)若P是这个二次函数图象上位于x轴下方的一点,且 ABP的面积为10,求点P的坐标.
ABP的面积为10,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点B(a,b)是第一象限内一点,且a、b满足等式a2-6a+9+|b-1|=0.

(1)求点B的坐标;
(2)如图,动点C以每秒1个单位长度的速度从O点出发,沿x轴的正半轴方向运动,同时动点A以每秒2个单位长度的速度从O点出发,沿y轴的正半轴方向运动,设运动的时间为t秒,当t为何值时,△ABC是AB为斜边的等腰直角三角形;
(3)如图,在(2)的条件下,作∠ABC的平分线BD,设BD的长为m,△ADB的面积为S.请用含m的式子表示S.
相关试题

