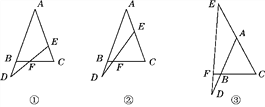
【题目】在等腰三角形ABC中,AB=AC,D是AB延长线上一点,E是AC上一点,DE交BC于点F.
(1)如图①,若BD=CE,求证:DF=EF.
(2)如图②,若BD=![]() CE,试写出DF和EF之间的数量关系,并证明.
CE,试写出DF和EF之间的数量关系,并证明.
(3)如图③,在(2)的条件下,若点E在CA的延长线上,那么(2)中结论还成立吗?试证明.
参考答案:
【答案】(1)证明见解析;(2)DF=![]() EF.(3)成立,证明见解析.
EF.(3)成立,证明见解析.
【解析】试题分析:
(1)在题图①中作EG∥AB交BC于点G,利用平行线的性质和等腰三角形的性质可证得:EG=EC;再证△BFD≌△GFE即可;
(2)在题图②中作EG∥AB交BC于点G,则∠D=∠FEG.同(1)可得EG=EC;
再证△BFD∽△GFE,利用相似三角形的性质即可证得:DF=![]() EF.
EF.
(3)在题图③中作EG∥AB交CB的延长线于点G,同(2)证:EG=EC,△BFD∽△GFE,再利用相似三角形的性质可得:DF=![]() EF,即(2)中的结论任然成立
EF,即(2)中的结论任然成立
试题解析:
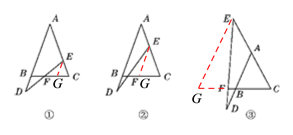
(1)在题图①中作EG∥AB交BC于点G,
则∠ABC=∠EGC,∠D=∠FEG.
∵AB=AC,∴∠ABC=∠C.
∴∠EGC=∠C.∴EG=EC.
∵BD=CE,∴BD=EG.
∵∠D=∠FEG,∠BFD=∠GFE,
∴△BFD≌△GFE.
∴DF=EF.
(2)解:DF=![]() EF.
EF.
在题图②中作EG∥AB交BC于点G,则∠D=∠FEG.由(1)得EG=EC.
∵∠D=∠FEG,∠BFD=∠EFG,
∴△BFD∽△GFE.
∴![]() .
.
∵BD=![]() CE=
CE=![]() EG,
EG,
∴DF=![]() EF.
EF.
(3)成立.
在题图③中作EG∥AB交CB的延长线于点G,
则仍有EG=EC,△BFD∽△GFE.
∴![]() ,
,
∵BD=![]() CE=
CE=![]() EG,
EG,
∴DF=![]() EF.
EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( )

A. (4,0) B. (5,0) C. (0,5) D. (5,5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠BCG=40°,求∠AGD的度数.

-
科目: 来源: 题型:
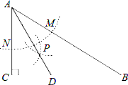
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法①AD是∠BAC的平分线;②∠ADC=60°③点D在AB的中垂线上;正确的个数是 个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛一枚均匀硬币正面朝上的概率为
 ,下列说法正确的是( )
,下列说法正确的是( )A. 连续抛一枚均匀硬币2次必有1次正面朝上
B. 连续抛一枚均匀硬币10次都可能正面朝上
C. 大量反复抛一枚均匀硬币,平均每100次出现下面朝上50次
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.一个游戏的中奖概率是
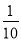 ,则做10次这样的游戏一定会中奖
,则做10次这样的游戏一定会中奖B.为了解全国中学生的心理健康情况,应该采用普查的方式
C.一组数据6,8,7,8,8,9,10的众数和中位数都是8
D.若甲组数据的方差S2甲=0.01,乙组数据的方差S2乙=0.1,则乙组数据比甲组数据稳定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
 中,点
中,点 是
是 边上的一个动点,连接
边上的一个动点,连接 .过点
.过点 作一条射线与边
作一条射线与边 的延长线交于点
的延长线交于点 ,使得
,使得 ,其中
,其中 是边
是边 延长线上的点.连接
延长线上的点.连接 .
.(
 )求证:
)求证:  是等腰直角三角形.
是等腰直角三角形.(
 )若
)若 ,求
,求 的面积.
的面积.
相关试题

