【题目】下列说法中正确的是( )
A.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为 ![]()
B.“对角线相等且相互垂直平分的四边形是正方形”这一事件是必然事件
C.“同位角相等”这一事件是不可能事件
D.“钝角三角形三条高所在直线的交点在三角形外部”这一事件是随机事件
参考答案:
【答案】B
【解析】解:A、掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为 ![]() ,故A错误; B、“对角线相等且相互垂直平分的四边形是正方形”这一事件是必然事件,故B正确;
,故A错误; B、“对角线相等且相互垂直平分的四边形是正方形”这一事件是必然事件,故B正确;
C、同位角相等是随机事件,故C错误;
D、“钝角三角形三条高所在直线的交点在三角形外部”这一事件是必然事件,故D错误;
故选:B.
【考点精析】关于本题考查的随机事件和列表法与树状图法,需要了解在条件S下,一定会发生的事件,叫相对于条件S的必然事件;在条件S下,一定不会发生的事件,叫相对于条件S的不可能事件;在条件S下可能发生也可能不发生的事件,叫相对于S的随机事件;当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率才能得出正确答案.
-
科目: 来源: 题型:
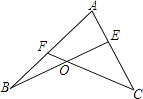
查看答案和解析>>【题目】已知:如图,点E在AC上,点F在AB上,BE,CF交于点O,且∠C=2∠B,∠BFC比∠BEC大20°,求∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师给出一个二次函数,甲、乙两名同学各指出这个函数的一个性质.甲:函数图象的顶点在x轴上;乙:抛物线开口向下;已知这两位同学的描述都正确,请你写出满足上述所有性质的一个二次函数表达式_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,△AOB为等腰直角三角形,A(4,4)
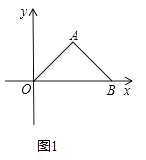
(1)求B点坐标;
(2)如图2,若C为x轴正半轴上一动点,以AC为直角边作等腰直角△ACD,∠ACD=90°连OD,求∠AOD的度数;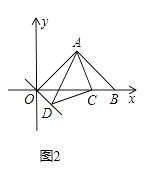
(3)如图3,过点A作y轴的垂线交y轴于E,F为x轴负半轴上一点,G在EF的延长线上,以EG为直角边作等腰Rt△EGH,过A作x轴垂线交EH于点M,连FM,等式AM=FM+OF是否成立?若成立,请证明:若不成立,说明理由.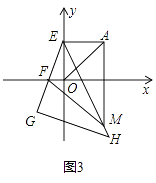
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P既在直线y=﹣3x﹣2上,又在直线y=2x+8上,则P点的坐标为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=(m﹣1)x+1的图象上两点A(x1,y1),B(x2,y2),当x1>x2时,有y1<y2,那么m的取值范围是( )
A. m>1 B. m<1 C. m>﹣1 D. m<﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题引入:
(1)如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);如图②,∠CBO=
 ∠ABC,∠BCO=
∠ABC,∠BCO= ∠ACB,∠A=α,则∠BOC= (用α表示)
∠ACB,∠A=α,则∠BOC= (用α表示)拓展研究:
(2)如图③,∠CBO=
 ∠DBC,∠BCO=
∠DBC,∠BCO= ∠ECB,∠A=α,请猜想∠BOC= (用α表示),并说明理由.
∠ECB,∠A=α,请猜想∠BOC= (用α表示),并说明理由.类比研究:
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=
 ∠DBC,∠BCO=
∠DBC,∠BCO= ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .
相关试题

