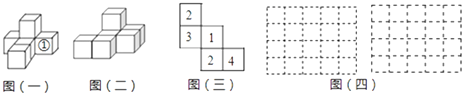
【题目】按要求完成问题:（1）如图（一），它是由6个同样大小的正方体摆成的几何体．将正方体①移走后，新几何体的三视图与原几何体的三视图相比，哪一个视图没有发生改变？

（2）如图（二），请你借助图四虚线网格画出该几何体的俯视图．

（3）如图（三），它是由几个小立方块组成的俯视图，小正方形上的数字表示该位置上的正方体的个数，请你借助图四虚线网格画出该几何体的主视图．

参考答案：

【答案】（1）如图（一），左视图没有发生改变；（2）如图1所示见解析，（3）如图2所示见解析．

【解析】

（1）利用结合体的形状，结合三视图可得出左视图没有发生变化；

（2）利用几何体的形状结合俯视图的得出得出答案；

（3）利用小立方体的个数结合俯视图得出主视图即可．

（1）如图（一），它是由6个同样大小的正方体摆成的几何体．将正方体①移走后，

新几何体的三视图与原几何体的三视图相比，左视图没有发生改变；

（2）如图1所示，（3）如图2所示．

关闭