【题目】“十 一”黄金周期间,我市庐山风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)、若9月30日的游客人数记为n,请用含n的代数式表示10月2日的游客________万人。
(2)、请判断七天内游客人数最多的是_______日;最少的是______日;它们相差_____万人。
(3)、以9月30日的游客人数为0点,用折线统计图表示这7天的游客人数变化情况:
参考答案:
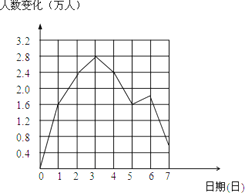
【答案】(1)a+2.4;(2)3,7,2.2;(3)如图所示:
【解析】
(1)从表格可看出10月2日的游客为a+1.6+0.8=a+2.4万人;
(2)3、7,
0.4+0.8+1.2﹣0.2=2.2,
相差2.2万人;
(3)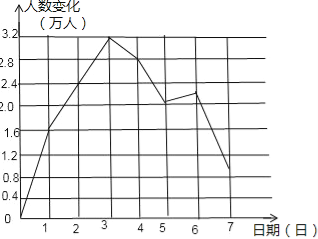
从表格可看出10月2日的游客为(a+1.6+0.8)万人;到3日游客是上升趋势,到7日基本是下降趋势,6日比五日增加点,但不多,4日到7日的人数变化和就是相差的人数;根据图表画折线统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:若关于x的一元一次方程ax=b的解为b+a,则称该方程为“和解方程”. 例如:方程2x=﹣4的解为x=﹣2,而﹣2=﹣4+2,则方程2x=﹣4为“和解方程”.
请根据上述规定解答下列问题:
(1)已知关于x的一元一次方程3x=m是“和解方程”,求m的值;
(2)已知关于x的一元一次方程﹣2x=mn+n是“和解方程”,并且它的解是x=n,求m,n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“为了安全,请勿超速”,如图所示是一条已经建成并通车的公路,且该公路的某直线路段MN上限速17m/s,为了检测来往车辆是否超速,交警在MN旁设立了观测点C.若某次从观测点C测得一汽车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200m.
(1)求观测点C到公路MN的距离;
(2)请你判断该汽车是否超速?(参考数据:
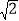 ≈1.41,
≈1.41,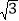 ≈1.73)
≈1.73)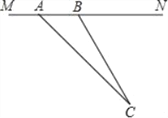
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体的长BE=15cm,宽AB=10cm,高AD=20cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x2+3x﹣2=0;
(2)(x﹣3)(x+1)=x﹣3. -
科目: 来源: 题型:
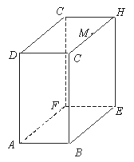
查看答案和解析>>【题目】A、B、C 为数轴上三点,若点 C 到点 A 的距离是点 C 到点 B 的距离的 2倍,则称点 C 是(A,B)的奇异点,例如图 1 中,点 A 表示的数为﹣1,点B 表示的数为 2,表示 1 的点 C 到点 A 的距离为 2,到点 B 的距离为 1,则点C 是(A,B)的奇异点,但不是(B,A)的奇异点.
(1)在图 1 中,直接说出点 D 是(A,B)还是(B,C)的奇异点;
(2)如图 2,若数轴上 M、N 两点表示的数分别为﹣2 和 4,(M,N)的奇异点 K 在 M、N 两点之间,请求出 K 点表示的数;
(3)如图 3,A、B 在数轴上表示的数分别为﹣20 和 40,现有一点 P 从点 B 出发,向左运动.
①若点 P 到达点 A 停止,则当点 P 表示的数为多少时,P、A、B 中恰有一个点为其余两点的奇异点?
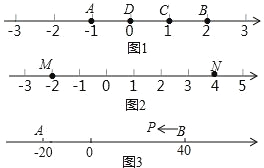
②若点 P 到达点 A 后继续向左运动,是否存在使得 P、A、B 中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时 PB 的距离;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.

(1)如果随机翻1张牌,那么抽中20元奖品的概率为 .
(2)如果随机翻2张牌,且第一次翻过的牌不再参加下次翻牌,请用列表或画树状图的方法求出所获奖品总值不低于30元的概率为多少?
相关试题

