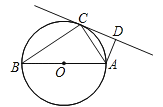
【题目】如图,AB是⊙O的直径,C是⊙O上一点,∠ACD=∠B,AD⊥CD.
(1)求证:CD是⊙O的切线;
(2)若AD=1,OA=2,求AC的值.
参考答案:
【答案】(1)证明见解析;(2)2.
【解析】
试题分析:(1)连接OC,由圆周角定理得出∠ACB=90°,由等腰三角形的性质得出∠B=∠BCO,证出∠OCD=∠OCA+∠BCO=∠ACB=90°,即可得出结论;
(2)证明△ACB∽△ADC,得出AC2=ADAB,即可得出结果.
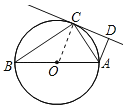
试题解析:(1)证明:连接OC,如图所示,∵AB是⊙O直径,∴∠ACB=90°,∵OB=OC,∴∠B=∠BCO,又∵∠ACD=∠B,∴∠OCD=∠OCA+∠ACD=∠OCA+∠BCO=∠ACB=90°,即OC⊥CD,∴CD是⊙O的切线;
(2)解:∵AD⊥CD,∴∠ADC=∠ACB=90°,又∵∠ACD=∠B,∴△ACB∽△ADC,∴AC2=ADAB=1×4=4,∴AC=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.x3?x﹣4=x﹣12
B.(x3)3=x6
C.2x2+x=x
D.(3x)﹣2=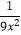
-
科目: 来源: 题型:
查看答案和解析>>【题目】在创建“全国文明城市”和“省级文明城区”过程中,栾城区污水处理厂决定先购买A、B两型污水处理设备共20台,对城区周边污水进行处理.已知每台A型设备价格为12万元,每台B型设备价格为10万元;1台A型设备和2台B型设备每周可以处理污水640吨,2台A型设备和3台B型设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)要想使污水处理厂购买设备的资金不超过230万元,但每周处理污水的量又不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】七年级学生小聪和小明完成了数学实验《钟面上的数学》之后,自制了一个模拟钟面,如图所示,O 为模拟钟面圆心,M、O、N 在一条直线上,指针 OA、OB 分别从 OM、ON 出发绕点 O 转动,OA 运动速度为每秒 15°,OB 运动速度为每秒 5°,当一根指针与起始位置重合时,运动停止,设转动的时间为 t 秒,请你试着解决他们提出的下列问题:
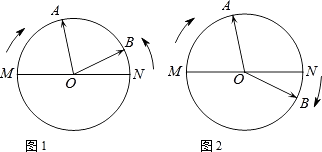
(1)若OA顺时针转动,OB逆时针转动,t=秒时,OA与OB第一次重合;
(2)若它们同时顺时针转动
①当 t=3 秒时,∠AOB=°; -
科目: 来源: 题型:
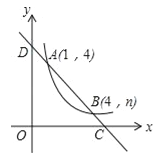
查看答案和解析>>【题目】如图,直线y=ax+b与反比例函数
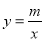 (x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点.
(x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点.(1)m= ,n= ;若M(
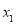 ,
,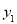 ),N(
),N(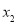 ,
,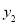 )是反比例函数图象上两点,且0<
)是反比例函数图象上两点,且0<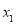 <
<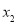 ,则
,则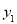
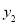 (填“<”或“=”或“>”);
(填“<”或“=”或“>”);(2)若线段CD上的点P到x轴、y轴的距离相等,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE,
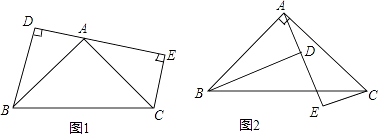
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,我们能得到什么结论?并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣1)2017+(﹣
 )﹣3﹣(2017)0的结果是( )
)﹣3﹣(2017)0的结果是( )
A.﹣10
B.﹣8
C.8
D.﹣9
相关试题

