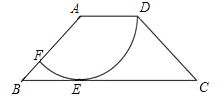
【题目】如图,在四边形ABCD中,AD∥BC,AD=2,AB=![]() ,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.
,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.
(1)求∠ABE的大小及![]() 的长度;
的长度;
(2)在BE的延长线上取一点G,使得![]() 上的一个动点P到点G的最短距离为
上的一个动点P到点G的最短距离为![]() ,求BG的长.
,求BG的长.
参考答案:
【答案】(1)45°,![]() ;(2)4.
;(2)4.
【解析】
试题分析:(1)连接AE,如图1,根据圆的切线的性质可得AE⊥BC,解Rt△AEB可求出∠ABE,进而得到∠DAB,然后运用圆弧长公式就可求出![]() 的长度;
的长度;
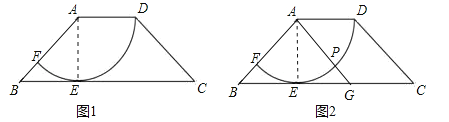
(2)如图2,根据两点之间线段最短可得:当A、P、G三点共线时PG最短,此时AG=AP+PG=![]() =AB,根据等腰三角形的性质可得BE=EG,只需运用勾股定理求出BE,就可求出BG的长.
=AB,根据等腰三角形的性质可得BE=EG,只需运用勾股定理求出BE,就可求出BG的长.
试题解析:(1)连接AE,如图1,∵AD为半径的圆与BC相切于点E,∴AE⊥BC,AE=AD=2.
在Rt△AEB中,sin∠ABE=![]() =
=![]() =
=![]() ,∴∠ABE=45°.∵AD∥BC,∴∠DAB+∠ABE=180°,∴∠DAB=135°,∴
,∴∠ABE=45°.∵AD∥BC,∴∠DAB+∠ABE=180°,∴∠DAB=135°,∴![]() 的长度为
的长度为![]() =
=![]() ;
;
(2)如图2,根据两点之间线段最短可得:当A、P、G三点共线时PG最短,此时AG=AP+PG=![]() =
=![]() ,∴AG=AB.∵AE⊥BG,∴BE=EG.∵BE=
,∴AG=AB.∵AE⊥BG,∴BE=EG.∵BE=![]() =
=![]() =2,∴EG=2,∴BG=4.
=2,∴EG=2,∴BG=4.
-
科目: 来源: 题型:
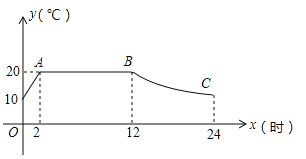
查看答案和解析>>【题目】我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线
 的一部分,请根据图中信息解答下列问题:
的一部分,请根据图中信息解答下列问题:(1)求k的值;
(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将100个数据分成八个组,如下表:
组号
一
二
三
四
五
六
七
八
频数
11
14
12
13
13
x
12
10
第六组的频数是( )
A. 12 B. 13 C. 14 D. 15
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知7,4,3,a,5这五个数的平均数是5,则a =______________
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校九年级1200学生的体重情况,请你运用所学的统计知识,将解决上述问题要经历的几个重要步骤进行排序.①收集数据;②设计调查问卷;③用样本估计总体;④整理数据;⑤分析数据.则正确的排序为 .(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一次函数y=x+b经过点A(0,3),那么b=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列长度的三根木棒首尾顺次连接,不能组成直角三角形的是( ).
A.8、15、17
B.7、24、25
C.3、4、5
D.2、3、 4
相关试题

