搜索
【题目】如图，正方形
的边长为4，点
是对角线
的中点，点
、
分别在
、
边上运动，且保持
，连接
，
，
.在此运动过程中，下列结论：①
；②
；③四边形
的面积保持不变；④当
时，
，其中正确的结论是（ ）
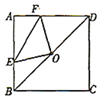
A.①②B.②③C.①②④D.①②③④
参考答案：
【答案】D
【解析】
过O
作
于G，
于
，由正方形的性质得到
，求得
，
，得到
，根据全等三角形的性质得到
，故①正确；
，推出
，故②正确；得到四边形
的面积
正方形
的面积
，四边形的面积保持不变；故③正确；根据平行线的性质得到
，
，求得
，得到
，于是得到
，故④正确．
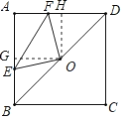
解：过O作于G，于H，
∵四边形
是正方形，
，
，
，
∵点O是对角线BD的中点，
，
，
，，
，
，
，
∴四边形
是正方形，
，
，
，
在
与
中，
，
，
，故①正确；
，
，
，故②正确；
，
∴四边形的面积正方形的面积，
∴四边形的面积保持不变；故③正确；
，
，，
，
，
，
，
，故④正确；
故选：
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】先阅读理解下面的例题，再按要求解答下列问题：
例题：解一元二次不等式
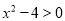.解∵
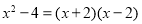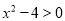，∴可化为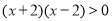
.由有理数的乘法法则：两数相乘，同号得正，得：①
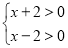②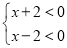
解不等式组①，得
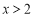，解不等式组②，得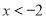
∴
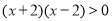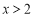的解集为或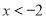.即一元二次不等式
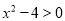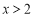的解集为或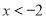.（1）一元二次不等式
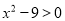的解集为____________；（2）试解一元二次不等式
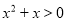；（3）试解不等式
. -
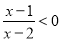科目： 来源： 题型：
查看答案和解析>>【题目】某超市销售樱桃，已知樱桃的进价为15元/千克，如果售价为20元/千克，那么每天可售出250千克，如果售价为25元/千克，那么每天可获利2000元，经调查发现：每天的销售量y（千克）与售价x（元/千克）之间存在一次函数关系．
（1）求y与x之间的函数关系式；
（2）若樱桃的售价不得高于28元/千克，请问售价定为多少时，该超市每天销售樱桃所获的利润最大？最大利润是多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】越来越多的人在用微信付款、转账，把微信账户里的钱转到银行卡叫做提现。
自2016年3月l日起，每个微信账户终身享有1000元的免费提现额度，当累计提现金额超过1000元时，累计提现金额超出1000元的部分需支付0.1%的手续费，以后每次提现支付的手续费为提现金额的0.1%.
（1）小明在今天第1次进行了提现，金额为l600元，他需支付手续费_________元；
（2）小亮自2016年3月1日至今，用自己的微信账户共提现3次，3次提现金额和手续费分别如下：
第1次
第2次
第3次
提现金额（元）
A
b
手续费（元）
0
0.4
3.4
问：小明3次提现金额各是多少元？
（3）单笔手续费小于0.1元的，按照0.1元收取（即提现不足100元，按照100元收取手续费）.小红至今共提现两次，每次提现金额都是整数，共支付手续费2.4元，第一次提现900元。求小红第二次提现金额的范围.
-
科目： 来源： 题型：
查看答案和解析>>【题目】射阳县实验初中为了解全校学生上学期参加社区活动的情况，学校随机调查了本校50名学生参加社区活动的次数，并将调查所得的数据整理如下：
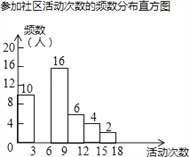
参加社区活动次数的频数、频率分布表
活动次数x
频数
频率
0＜x≤3
10
0.20
3＜x≤6
a
0.24
6＜x≤9
16
0.32
9＜x≤12
6
0.12
12＜x≤15
m
b
15＜x≤18
2
n
根据以上图表信息，解答下列问题：
（1）表中a= ，b= ；
（2）请把频数分布直方图补充完整（画图后请标注相应的数据）；
（3）若该校共有1200名学生，请估计该校在上学期参加社区活动超过6次的学生有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店在今年2月底以每袋23元的成本价收购一批农产品准备向外销售，当此农产品售价为每袋36元时，3月份销售125袋，4、5月份该农产品十分畅销，销售量持续走高.在售价不变的基础上，5月份的销售量达到180袋.设4、5这两个月销售量的月平均增长率不变.
（1）求4、5这两个月销售量的月平均增长率；
（2）6月份起，该商店采用降价促销的方式回馈顾客，经调查发现，该农产品每降价1元/袋，销量就增加4袋，当农产品每袋降价多少元时，该商店6月份获利1920元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解，并规定：F（n）=
，例如12可以分解成1×12,2×6或3×4，因为12-1＞6-2＞4-3，所有3×4是最佳分解，所以F（12）=
.（1）如果一个正整数a是另外一个正整数b的平方，我们称正整数a是完全平方数，求证：对任意一个完全平方数m，总有F（m）=1.
（2）如果一个两位正整数t，t=10x+y（1≤x≤y≤9,x,y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18，那么我们称这个数t为“吉祥数”，求所有“吉祥数”中F（t）的最大值.
相关试题
