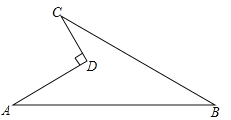
【题目】如图所示的一块地,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m,求这块地的面积.
参考答案:
【答案】24.
【解析】试题分析:连接AC,利用勾股定理及逆定理可以得出三角形ACD和ABC是直角三角形,△ABC的面积减去△ACD的面积就是所求的面积.
试题解析:解:连接AC .
在Rt△ACD中,AD=4,CD=3,∴AC 2 =AD 2 +CD 2 =4 2 +3 2 =25,又∵AC>0,∴AC=5.
又∵BC=12,AB=13,∴AC 2 +BC 2 =5 2 +12 2 =169,又∵AB 2 =169,∴AC 2 +BC 2 =AB 2 ,∴△ACB是直角三角形,∴S=S △ABC -S △ADC =30-6=24(m2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有三个点A、B、C,请回答下列问题.
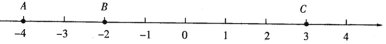
(1)A、B、C三点分别表示什么数?它们到原点的距离分别是多少?
(2)将点B向左移动3个单位长度后,三个点所表示的数中最小的数是多少?
(3)将点A向右移动4个单位长度后,三个点所表示的数中最小的数是多少?
(4)要怎样移动A、B、C三点中的两个点,才能使三个点表示的数相同?移动方法唯一吗?若不是,请任意选择一种回答,
-
科目: 来源: 题型:
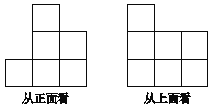
查看答案和解析>>【题目】用大小相同的小立方块搭成一个几何体,使得从正面和上面看到的几何体的形状图如图19所示.
(1)这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?
(2)画出这两种情况下从左面看到的几何体的形状图.(各画出一种即可)
-
科目: 来源: 题型:
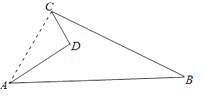
查看答案和解析>>【题目】如图①有一个宝塔,它的地基边缘是周长为26m的正五边形ABCDE(如图②),点O为中心.(下列各题结果精确到0.1m)

(1)求地基的中心到边缘的距离;
(2)己知塔的墙体宽为1m,现要在塔的底层中心建一圆形底座的塑像,并且留出最窄处为1.6m的观光通道,问塑像底座的半径最大是多少? -
科目: 来源: 题型:
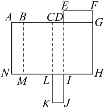
查看答案和解析>>【题目】如图所示是长方体的平面展开图.
(1)将平面展开图折叠成一个长方体,与字母N重合的点有哪几个?
(2)若AG=CK=14 cm,FG=2 cm,LK=5 cm,则该长方体的表面积和体积分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体由几个棱长均为1的小正方体搭成,从上面看到的几何体的形状图如图(1)所示,正方形中的数字表示该位置的小正方体的个数.
(1)请在图(2)的方格纸中画出从正面看和从左面看到的几何体的形状图;
(2)根据从三个方向看到的几何体的形状图,请你计算该几何体的表面积为________平方单位(包含底面);
(3)若从上面看到的几何体的形状图不变,几何体各位置的小正方体的个数可以改变,则搭成这样的几何体的表面积最大为________平方单位(包含底面).

图(1) 图(2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=3,AC=4,BC=5,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )
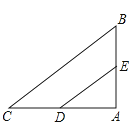
A.相切
B.相交
C.相离
D.无法确定
相关试题

