【题目】如图,在平面直角坐标系xOy中,已知点A(0,8),B(6,0),点C(3,a)在线段AB上.
(1)则a的值为________;
(2)若点D(-4,3),求直线CD的函数表达式;
(3)点(-5,-4)在直线CD上吗?说明理由.

参考答案:
【答案】4
【解析】(1)利用待定系数法求出AB的解析式,然后把点C坐标代入即可得;
(2)由C、D的坐标,利用待定系数法即可求得直线CD的解析式;
(3)把x=-5代入直线CD解析式,通过计算比较即可得..
(1)设直线AB的解析式为y=mx+n,
把A(0,8)、B(6,0)分别代入得:![]() ,
,
解得: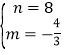 ,
,
所以直线AB的解析式为:y=![]() x+8,
x+8,
由点C(3,a)在线段AB上,则有a=-4+8=4,
故答案为:4;
(2)设直线CD的函数表达式为y=kx+b,
将C(3,4),D(-4,3)代入得![]() ,
,
解得: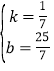 ,故直线CD的函数表达式为y=
,故直线CD的函数表达式为y=![]() x+
x+![]() ;
;
(3)点(-5,-4)不在直线CD上,理由如下:
当x=-5时,y=![]() ×(-5)+
×(-5)+![]() =
=![]() ≠-4,
≠-4,
∴点(-5,-4)不在直线CD上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOC:∠COD:∠BOD=2:3:4,且A,O,B三点在一条直线上,OE,OF分别平分∠AOC和∠BOD,OG平分∠EOF,求∠GOF的度数.将下列解题过程补充完整.
解:因为,∠AOC:∠COD:∠BOD=2:3:4,
所以∠AOC= ,∠COD= ,∠BOD= ,
因为OE,OF分别平分∠AOC和∠BOD,
所以∠AOE= ,∠BOF= ,
所以∠EOF= ,
又因为 ,所以∠GOF=60°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.
(1)求y关于x的函数解析式;
(2)若某用户二、三月份共用水40m3(二月份用水量不超过25m3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?

-
科目: 来源: 题型:
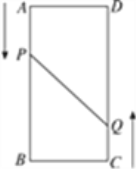
查看答案和解析>>【题目】如图,A,B,C,D为矩形的四个顶点,AB=16 cm,BC=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,点Q以2 cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.问几秒时点P和点Q的距离是10 cm?
-
科目: 来源: 题型:
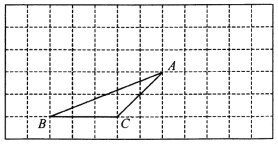
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长为1个单位长度,三角形ABC的顶点都在格点上,将三角形ABC向右平移2个单位长度,再向上平移3个单位长度,得到三角形A′B′C′
(1)请在图中画出三角形A′B′C′;
(2)求三角形ABC的面积;
(3)若AC的长约为2.8,则边AC上的高约为多少?(结果保留分数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,点P为直线
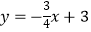 上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是
上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是
相关试题

