【题目】某段公路经测算发现,匀速行驶的车辆通过该段公路时,所需时间![]() (h)与行驶速度
(h)与行驶速度![]() (km/h)满足反比例函数关系,其图象为如图所示的一段曲线,且端点为A(40,1)和B(m,0.5).
(km/h)满足反比例函数关系,其图象为如图所示的一段曲线,且端点为A(40,1)和B(m,0.5).

(1)求![]() 与
与![]() 的函数关系式及m的值;
的函数关系式及m的值;
(2)若该段公路限速50km/h,求通过该路段需要的最短时间和这段公路的长.
参考答案:
【答案】(1)![]()
(2)0.8h,40km
【解析】(1)设t与y的函数关系式为t=![]() (k≠0)把A的坐标代入解析式,利用待定系数法求得函数解析式,然后爸爸(m,0.5)代入解析式求得m的值;
(k≠0)把A的坐标代入解析式,利用待定系数法求得函数解析式,然后爸爸(m,0.5)代入解析式求得m的值;
(2)求得当y=50时t的值,根据图象即可作出解答.
解:(1)由题意:可设t与y的函数关系式为t=![]() (k≠0),
(k≠0),
∵函数t=![]() 经过点A(40, 1),
经过点A(40, 1),
∴1=![]() ,解得k=40,
,解得k=40,
∴t与y的函数关系式为t=![]() ;
;
把B(m,0.5)代入t=![]() ,
,
得0.5=![]() ,解得m=80;
,解得m=80;
(2)把y=50代入t=![]() ,得t=
,得t=![]() =0.8,
=0.8,
则通过该路段需要的最短时间是0.8小时,这段公路的长为40km.
“点睛”本题考查了反比例函数的实际应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式x-4<0的解集是________.
-
科目: 来源: 题型:
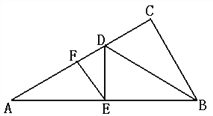
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,DE⊥AB于E,EF∥AC于F。
(1)求证:△EDF∽△ADE;
(2)猜想:线段DC、DF、DA之间存在什么关系?并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将函数y=2x2的图象先向右平移1个单位长度,再向上平移5个单位长度,所得图象的函数解析式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当k=_____时二次三项式x2﹣2(k+3)x+k+5是一个完全平方式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】无理数是( )
A. 带根号的数 B. 无限循环小数
C. 无限不循环小数 D. 开不尽方的数
-
科目: 来源: 题型:
查看答案和解析>>【题目】画出数轴,把22 , 0,﹣2,(﹣1)3 , ﹣|﹣3.5|,
 这六个数在数轴上表示出来;按从小到大的顺序用“<”号将各数连接起来.
这六个数在数轴上表示出来;按从小到大的顺序用“<”号将各数连接起来.
相关试题

