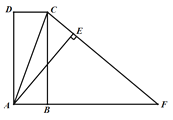
【题目】如图,已知四边形ABCD是矩形,延长AB至点F,连结CF,使得CF=AF,过点A作AE⊥FC于点E.
(1)求证:AD=AE.
(2)连结CA,若∠DCA=70°,求∠CAE的度数.

参考答案:
【答案】(1)证明见解析;(2)20°
【解析】证明:(1)∵CF=AF,∴∠FCA=∠CAF
∵四边形ABCD是矩形 , ∴ DC∥AB ∴ ∠DCA=∠CAF ,
∴∠FCA=∠DCA
∵AE⊥FC ∴∠CEA=90°∴∠CDA=∠CEA=90°,
又∵CA=CA,∴△ADC≌△CAE ∴AD=AE
(方法不限,也可以先证△CBF≌△ABE)
(2)∵△ADC≌△CAE ∴∠CAE=∠CAD
∵四边形ABCD是矩形 ,∴∠D=90°
∴∠CAD=![]()
∴∠CAE=20°
-
科目: 来源: 题型:
查看答案和解析>>【题目】据报道,2014中国军费预算比上年上涨了12.2%,而美国军费预算比上年下降了1.2%,比较两国军费预算( )
A.中国军费多
B.美国军费多
C.两国一样多
D.条件不足,不能判断 -
科目: 来源: 题型:
查看答案和解析>>【题目】中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对七年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本书最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表,如下所示:
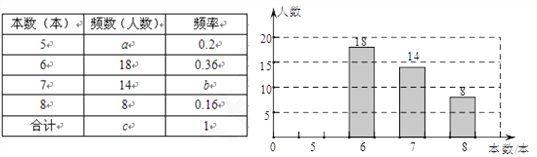
(1)统计表中的a=________,b=___________,c=____________;
(2)请将频数分布表直方图补充完整;
(3)求所有被调查学生课外阅读的平均本数;
(4)若该校七年级共有1200名学生,请你分析该校七年级学生课外阅读7本及以上的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C.
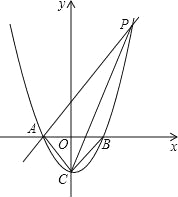
(1)求A、B、C三点的坐标;
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积;
(3)在x轴上方的抛物线上是否存在一点M,过M作MG⊥x轴于点G,使以A、M、G三点为顶点的三角形与△PCA相似?若存在,请求出M点的坐标;否则,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的调查,适合用实验方法的是( )
A.推荐班长候选人
B.调查同学们的生日
C.你在10秒内能跑多少米
D.世界上发生的“禽流感”的情况 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=kx的图象经过点A(﹣1,2),则正比例函数的解析式为 .
-
科目: 来源: 题型:
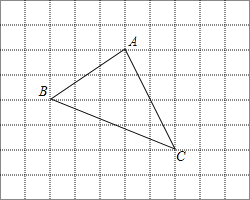
查看答案和解析>>【题目】如图是一个被抹去x轴、y轴及原点O的网格图,网格中每个小正方形的边长均为1个单位长度,三角形ABC的各顶点都在网格的格点上,若记点A的坐标为(﹣1,3),点C的坐标为(1,﹣1).
(1)请在图中找出x轴、y轴及原点O的位置;
(2)把△ABC向下平移2个单位长度,再向右平移3个单位长度,请你画出平移后的△A1B1C1,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是 ;
(3)试求出△ABC的面积.
相关试题

