搜索
【题目】已知正比例函数y=kx的图象经过点A（﹣1，2），则正比例函数的解析式为 ．
参考答案：
【答案】y=﹣2x
【解析】
试题根据点在直线上点的坐标满足方程的关系，把点A的坐标代入函数解析式求出k值即可得解：
∵正比例函数y=kx的图象经过点A（﹣1，2），
∴﹣k=2，即k=﹣2。
∴正比例函数的解析式为y=﹣2x。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知抛物线y=x2-1与x轴交于A、B两点，与y轴交于点C．
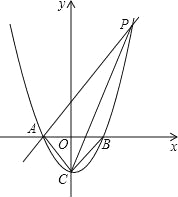
（1）求A、B、C三点的坐标；
（2）过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积；
（3）在x轴上方的抛物线上是否存在一点M，过M作MG⊥x轴于点G，使以A、M、G三点为顶点的三角形与△PCA相似？若存在，请求出M点的坐标；否则，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知四边形ABCD是矩形，延长AB至点F，连结CF，使得CF=AF，过点A作AE⊥FC于点E.
（1）求证：AD=AE.
（2）连结CA，若∠DCA=70°，求∠CAE的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面的调查，适合用实验方法的是（ ）
A.推荐班长候选人
B.调查同学们的生日
C.你在10秒内能跑多少米
D.世界上发生的“禽流感”的情况 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图是一个被抹去x轴、y轴及原点O的网格图，网格中每个小正方形的边长均为1个单位长度，三角形ABC的各顶点都在网格的格点上，若记点A的坐标为（﹣1，3），点C的坐标为（1，﹣1）．
（1）请在图中找出x轴、y轴及原点O的位置；
（2）把△ABC向下平移2个单位长度，再向右平移3个单位长度，请你画出平移后的△A1B1C1，若△ABC内部一点P的坐标为（a，b），则点P的对应点P1的坐标是 ；
（3）试求出△ABC的面积．
-
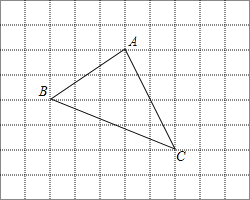
科目： 来源： 题型：
查看答案和解析>>【题目】如图甲，在△ABC中，∠ACB为锐角，点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF，解答下列问题：
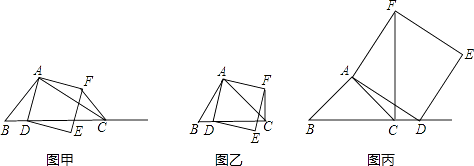
（1）如果AB=AC，∠BAC=90°．
①当点D在线段BC上时（与点B不重合），如图乙，线段CF、BD之间的位置关系是什么？写出它们之间的数量关系．
②当点D在线段BC的延长线上时，如图丙，①中的结论是否仍然成立，请证明？
（2）如果AB≠AC，∠BAC≠90°，点D在线段BC上运动．试探究：当△ABC满足一个什么条件时，CF⊥BC（点C、F重合除外）？直接写出条件，不需要证明．
（3）若AC=4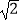
，BC=3，在（2）的条件下，求△ABC中AB边上的高． -
科目： 来源： 题型：
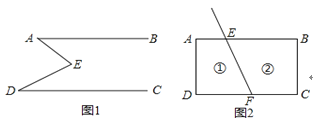
查看答案和解析>>【题目】如图1，E是直线AB，CD内部一点，AB∥CD，连接EA，ED．
（1）探究猜想：①若∠A=30°，∠D=40°，则∠AED等于多少度？
②若∠A=20°，∠D=60°，则∠AED等于多少度？
③猜想图1中∠AED，∠EAB，∠EDC的关系并证明你的结论．
（2）拓展应用：如图2，线段FE与长方形ABCD的边AB交于点E，与边CD 交于点F．图2中①②分别是被线段FE隔开的2个区域（不含边界），P是位于以上两个区域内的一点，猜想∠PEB，∠PFC，∠EPF的关系（不要求说明理由）．
相关试题
