【题目】如图,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,过点A作AG⊥EB,垂足为G,AG交BD于F,则OE=OF.
(1)请证明0E=OF
(2)解答(1)题后,某同学产生了如下猜测:对上述命题,若点E在AC的延长线上,AG⊥EB,AG交 EB的延长线于 G,AG的延长线交DB的延长线于点F,其他条件不变,则仍有OE=OF.问:猜测所得结论是否成立?若成立,请给出证明;若不成立,请说明理由.

参考答案:
【答案】(1)证明见解析;(2)当点E在AC的延长线上时,OE=OF仍成立.
【解析】试题分析:(1)根据正方形对角线的性质可得AC⊥BD,∠OAF+∠AFO=90°,
因为AG⊥BE,所以∠EBO+∠BFG=90°,因为∠BFG=∠AFO,所以∠OAF=∠EBO,
因为∠AOF=∠BOE,AO=BO,所以△AOF≌△BOE,所以OE=OF,
(2)根据正方形对角线的性质,可得:AC⊥BD,即可求出∠OAF+∠AFO=90°,
因为AG⊥BE,所以∠BEO+∠EAG=90°,所以∠AFO=∠BEO,因为∠AOF=∠BOE,AO=BO,
所以△AOF≌△BOE,所以OE=OF.
试题解析:(1)证明:∵正方形ABCD中对角线AC、BD相交于O,

∴AC⊥BD,
∴∠OAF+∠AFO=90°,
∵AG⊥BE,
∴∠EBO+∠BFG=90°,
∵∠BFG=∠AFO,
∴∠OAF=∠EBO,
∵∠AOF=∠BOE,AO=BO,
∴△AOF≌△BOE,
∴OE=OF,
(2)解:当点E在AC的延长线上时,OE=OF仍成立,
证明:∵正方形ABCD中对角线AC,BD相交于O,
∴AC⊥BD,
∴∠OAF+∠AFO=90°,
∵AG⊥BE,
∴∠BEO+∠EAG=90°,
∴∠AFO=∠BEO,
∵∠AOF=∠BOE,AO=BO,
∴△AOF≌△BOE,
∴OE=OF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(
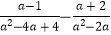 )÷(
)÷( 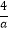 ﹣1),其中a是满足不等组
﹣1),其中a是满足不等组 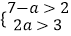 的整数解.
的整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习了数据的收集、整理与描述后,为妈妈整理记录了10月份的家庭支出情况,并绘制成如下尚不完整的统计图表,请你根据图表信息完成下列各题:
项目
物业费
伙食费
服装费
其他费
金额/元
800
400

(1)10月份小明家共支出多少元?
(2)在扇形统计图中,表示“其他费”的扇形圆心角为多少度?
(3)请将表格补充完整;项目
物业费
伙食费
服装费
其他费
金额/元
800
400
(4)请将条形统计图补充完整. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为31°,塔底B的仰角为26.6°.已知塔高BC=40米,塔所在的山高OB=240米,OA=300米,图中的点O、B、C、A、P在同一平面内.求:
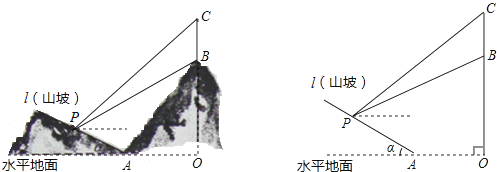
(1)P到OC的距离.
(2)山坡的坡度tanα.
(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin31°≈0.52,tan31°≈0.60) -
科目: 来源: 题型:
查看答案和解析>>【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图示,三角形ABC是等边三角形,D是BC边上的一点,三角形ABD经过旋转后到达三角形ACE的位置.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M到了什么位置?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,回答下列问题:
(1)比较∠FOD与∠FOE的大小;
(2)借助三角板比较∠DOE与∠BOF的大小;
(3)借助量角器比较∠AOE与∠DOF的大小.

相关试题

