Question

【题目】如图,,,点D在边BC上与B、C不重合,四边形ADEF为正方形,过点F作,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论：；：：2；；,其中正确的结论的个数是()

A.1B.2C.3D.4

Answer 1

【答案】D

【解析】

由正方形的性质得出∠FAD=90°，AD=AF=EF，证出∠CAD=∠AFG，由AAS证明△FGA≌△ACD，得出AC=FG，①正确；
证明四边形CBFG是矩形，得出S△FAB=FBFG=S四边形CBFG，②正确；
由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°，③正确；
证出△ACD∽△FEQ，得出对应边成比例，得出DFE=AD2=FQAC，④正确．

解：∵四边形ADEF为正方形，
∴∠FAD=90°，AD=AF=EF，
∴∠CAD+∠FAG=90°，
∵FG⊥CA，
∴∠GAF+∠AFG=90°，
∴∠CAD=∠AFG，
在△FGA和△ACD中，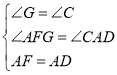

∴△FGA≌△ACD（AAS），
∴AC=FG，①正确；
∵BC=AC，
∴FG=BC，
∵∠ACB=90°，FG⊥CA，
∴FG∥BC，
∴四边形CBFG是矩形，
∴∠CBF=90°，S△FAB=FBFG=S四边形CBFG，②正确；
∵CA=CB，∠C=∠CBF=90°，
∴∠ABC=∠ABF=45°，③正确；
∵∠FQE=∠DQB=∠ADC，∠E=∠C=90°，
∴△ACD∽△FEQ，
∴AC：AD=FE：FQ，
∴ADFE=AD2=FQAC，④正确；

所以①②③④正确．

故选：D.