【题目】有一组邻边相等,并且有一个角是直角的平行四边形是正方形,因此正方形是四边相等,四角相等的四边形.
初二数学兴趣小组开展了一次课外活动,过程如下:如图,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.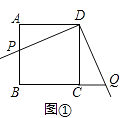
(1)求证:DP=DQ
(2)如图②,小聪在图①的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;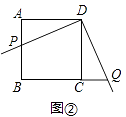
(3)如图③,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小聪算出△DEP的面积.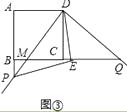
参考答案:
【答案】
(1)
证明:∵∠ADC=∠PDQ=90°,
∴∠ADP=∠CDQ.
在△ADP与△CDQ中, 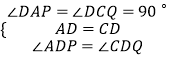
∴△ADP≌△CDQ(ASA),
∴DP=DQ
(2)
证明:猜测:PE=QE.
证明:由(1)可知,DP=DQ.
在△DEP与△DEQ中, 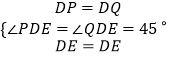
∴△DEP≌△DEQ(SAS),
∴PE=QE
(3)
解:∵AB:AP=3:4,AB=6,
∴AP=8,BP=2.
与(1)同理,可以证明△ADP≌△CDQ,
∴CQ=AP=8.
与(2)同理,可以证明△DEP≌△DEQ,
∴PE=QE.
设QE=PE=x,则BE=BC+CQ﹣QE=14﹣x.
在Rt△BPE中,由勾股定理得:BP2+BE2=PE2,
即:22+(14﹣x)2=x2,
解得:x= ![]() ,即QE=
,即QE= ![]() .
.
∴S△DEQ= ![]() QECD=
QECD= ![]() ×
× ![]() ×6=
×6= ![]() .
.
∵△DEP≌△DEQ,
∴S△DEP=S△DEQ= ![]()
【解析】(1)证明△ADP≌△CDQ,即可得到结论:DP=DQ;(2)证明△DEP≌△DEQ,即可得到结论:PE=QE;(3)与(1)(2)同理,可以分别证明△ADP≌△CDQ、△DEP≌△DEQ.在Rt△BPE中,利用勾股定理求出PE(或QE)的长度,从而可求得S△DEQ= ![]() ,而△DEP≌△DEQ,所以S△DEP=S△DEQ
,而△DEP≌△DEQ,所以S△DEP=S△DEQ ![]() .
.
【考点精析】掌握全等三角形的性质是解答本题的根本,需要知道全等三角形的对应边相等; 全等三角形的对应角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2+1先向左平移2个单位,再向下平移4个单位,那么所得到的抛物线的函数关系式是( )
A.y=(x+2)2+3
B.y=(x+2)2﹣3
C.y=(x﹣2)2+3
D.y=(x﹣2)2﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】在中俄“海上联合—2014”反潜演习中,我军舰A测得潜艇C的俯角为300.位于军舰A正上方1000米的反潜直升机B侧得潜艇C的俯角为680,试根据以上数据求出潜艇C离开海平面的下潜深度。(结果保留整数。参考数据:sin680≈0.9,cos680≈0.4,,tan680≈2.5.
 ≈1.7)
≈1.7)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在网格图中建立平面直角坐标系,
 的顶点坐标为
的顶点坐标为 、
、 、
、 .
.
(1)若将
 向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的
向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的 ;
;(2)画出
 绕C1顺时针方向旋转900后得到的
绕C1顺时针方向旋转900后得到的 ;
;(3)
 与
与 是中心对称图形,请写出对称中心的坐标: ;并计算
是中心对称图形,请写出对称中心的坐标: ;并计算 的面积: .
的面积: .(4)在坐标轴上是否存在P点,使得△PAB与△CAB的面积相等,若有,则求出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
在一个三角形中,各边和它所对角的正弦的比相等, =
= =
= ,利用上述结论可以求解如下题目:
,利用上述结论可以求解如下题目:
在△ABC中,∠A、∠B、∠C的对边分别为a,b,c.若∠A=45°,∠B=30°,a=6,求b.
解:在△ABC中,∵ =
= ∴b=
∴b= =
= =
= =3
=3 .
.
理解应用:
如图,甲船以每小时30 海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10 海里.
海里.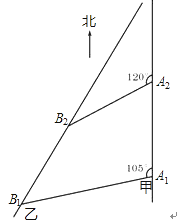
(1)判断△A1A2B2的形状,并给出证明
(2)求乙船每小时航行多少海里? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列单项式中,与a2b是同类项的是( )
A.2a2b
B.a2b2
C.ab2
D.3ab -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣6+(﹣12)÷(﹣3)
(2)﹣32×5﹣(﹣2)3÷4
相关试题

