【题目】如图,![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,如果
,如果![]() ,
,![]() ,那么
,那么![]() 的长为________
的长为________![]() ,
,![]() 的长为_______
的长为_______![]() .
.

参考答案:
【答案】4 3
【解析】
依据△ACD≌△AED(AAS),即可得到AC=AE=6cm,CD=ED,再根据勾股定理可得AB的长,进而得出EB的长;设DE=CD=x,则BD=8-x,依据勾股定理可得,Rt△BDE中,DE2+BE2=BD2,解方程即可得到DE的长.
∵AD平分∠CAB,
∴∠CAD=∠EAD,
又∵∠C=90°,DE⊥AB,
∴∠C=∠AED=90°,
又∵AD=AD,
∴△ACD≌△AED(AAS),
∴AC=AE=6cm,CD=ED,
∵Rt△ABC中,AB=![]() =10(cm),
=10(cm),
∴BE=AB-AE=10-6=4(cm),
设DE=CD=x,则BD=8-x,
∵Rt△BDE中,DE2+BE2=BD2,
∴x2+42=(8-x)2,
解得x=3,
∴DE=3cm,
故答案为:4,3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着北京申办冬奥会的成功,愈来愈多的同学开始关注我国的冰雪体育项目. 小健从新闻中了解到:在2018年平昌冬奥会的短道速滑男子500米决赛中,中国选手武大靖以39秒584的成绩打破世界纪录,收获中国男子短道速滑队在冬奥会上的首枚金牌. 同年11月12日,武大靖又以39秒505的成绩再破世界纪录. 于是小健对同学们说:“2022年北京冬奥会上武大靖再获金牌的可能性大小是
 .”你认为小健的说法_________(填“合理”或“不合理”),理由是__________________________.
.”你认为小健的说法_________(填“合理”或“不合理”),理由是__________________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】若我们规定三角“
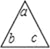 ”表示为:abc;方框“
”表示为:abc;方框“ ”表示为:(xm+yn).例如:
”表示为:(xm+yn).例如: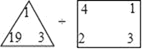 =1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
=1×19×3÷(24+31)=3.请根据这个规定解答下列问题:(1)计算:
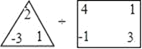 = ______ ;
= ______ ;(2)代数式
 为完全平方式,则k= ______ ;
为完全平方式,则k= ______ ;(3)解方程:
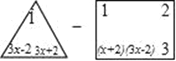 =6x2+7.
=6x2+7. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图是用4个全等的长方形拼成的一个“回形”正方形,图中阴影部分面积用2种方法表示可得一个等式,这个等式为_______.
(2)若(4x﹣y)2=9,(4x+y)2=169,求xy的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
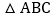 中,点
中,点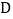 在
在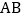 边上,
边上,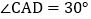 ,
,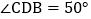 .给出下列三组条件(每组条件中的线段的长度已知):①
.给出下列三组条件(每组条件中的线段的长度已知):①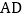 ,
,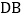 ;②
;②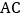 ,
,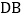 ;③
;③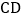 ,
,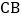 ;能使
;能使 唯一确定的条件的序号为( )
唯一确定的条件的序号为( )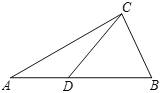
A. ①② B. ①③ C. ②③ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )

A.5
B.4
C.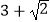
D.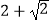
-
科目: 来源: 题型:
查看答案和解析>>【题目】若我们规定三角“
 ”表示为:abc;方框“
”表示为:abc;方框“ ”表示为:(xm+yn).例如:
”表示为:(xm+yn).例如: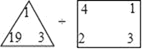 =1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
=1×19×3÷(24+31)=3.请根据这个规定解答下列问题:(1)计算:
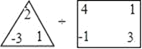 = ______ ;
= ______ ;(2)代数式
 为完全平方式,则k= ______ ;
为完全平方式,则k= ______ ;(3)解方程:
 =6x2+7.
=6x2+7.
相关试题

