
【题目】如图所示,在△ABC中,![]() ,D、E分别是边AB、BC上的动点,且
,D、E分别是边AB、BC上的动点,且![]() ,连结AD、AE,点M、N、P分别是CD、AE、AC的中点,设
,连结AD、AE,点M、N、P分别是CD、AE、AC的中点,设![]() .
.
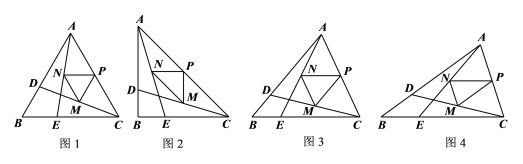
(1)观察猜想
①在求![]() 的值时,小明运用从特殊到一般的方法,先令
的值时,小明运用从特殊到一般的方法,先令![]() ,解题思路如下:
,解题思路如下:
如图1,先由![]() ,得到
,得到![]() ,再由中位线的性质得到
,再由中位线的性质得到![]() ,
,
![]() ,进而得出△PMN为等边三角形,∴
,进而得出△PMN为等边三角形,∴![]() .
.
②如图2,当![]() ,仿照小明的思路求
,仿照小明的思路求![]() 的值;
的值;
(2)探究证明
如图3,试猜想![]() 的值是否与
的值是否与![]() 的度数有关,若有关,请用含
的度数有关,若有关,请用含![]() 的式子表示出
的式子表示出![]() ,若无关,请说明理由;
,若无关,请说明理由;
(3)拓展应用
如图4,![]() ,点D、E分别是射线AB、CB上的动点,且
,点D、E分别是射线AB、CB上的动点,且![]() ,点M、N、P分别是线段CD、AE、AC的中点,当
,点M、N、P分别是线段CD、AE、AC的中点,当![]() 时,请直接写出MN的长.
时,请直接写出MN的长.
【答案】(1)②![]() ;(2)
;(2)![]() 的值与
的值与![]() 的度数有关,
的度数有关,![]() ;(3)MN的长为
;(3)MN的长为![]() 或
或![]() .
.
【解析】
(1)②先根据线段的和差求出![]() ,再根据中位线定理、平行线的性质得出
,再根据中位线定理、平行线的性质得出![]() ,从而可得出
,从而可得出![]() ,然后根据等腰直角三角形的性质即可得;
,然后根据等腰直角三角形的性质即可得;
(2)参照题(1)的方法,得出![]() 为等腰三角形和
为等腰三角形和![]() 的度数,再利用等腰三角形的性质即可求出答案;
的度数,再利用等腰三角形的性质即可求出答案;
(3)分两种情况:当点D、E分别是边AB、CB上的动点时和当点D、E分别是边AB、CB的延长线上的动点时,如图(见解析),先利用等腰三角形的性质与判定得出![]() ,再根据相似三角形的判定与性质得出BC、CE的长,由根据等腰三角形的三线合一性得出
,再根据相似三角形的判定与性质得出BC、CE的长,由根据等腰三角形的三线合一性得出![]() ,从而可得
,从而可得![]() 的值,最后分别利用(2)的结论即可得MN的长.
的值,最后分别利用(2)的结论即可得MN的长.
(1)②![]()
∴![]()
![]()
∴![]() 为等腰直角三角形,
为等腰直角三角形,![]()
∵点M、N、P分别是CD、AE、AC的中点
![]()
![]()
∴![]()
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]()
即![]() ;
;
(2)![]() 的值与
的值与![]() 的度数有关,求解过程如下:
的度数有关,求解过程如下:
由(1)可知,![]() ,即
,即![]() 为等腰三角形
为等腰三角形
![]()
如图5,作![]()
则![]()
在![]() 中,
中,![]() ,即
,即
则![]() ;
;
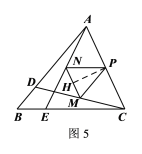
(3)依题意,分以下两种情况:
①当点D、E分别是边AB、CB上的动点时
如图6,作![]() 的角平分线交AB边于点F,并连结BP
的角平分线交AB边于点F,并连结BP
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() ,即
,即![]()
设![]() ,则
,则![]()
![]()
解得![]() 或
或![]() (不符题意,舍去)
(不符题意,舍去)
即![]()
![]()
由(2)可知,![]()
![]()
![]() 点P是AC上的中点
点P是AC上的中点
![]() ,
,![]() (等腰三角形的三线合一)
(等腰三角形的三线合一)
在![]() 中,
中,![]() ,即
,即![]()
![]()
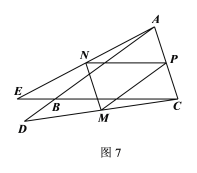
②如图7,当点D、E分别是边AB、CB的延长线上的动点时
同理可得:![]()
![]()
![]()
综上,MN的长为![]() 或
或![]() .
.



科目:初中数学 来源: 题型:
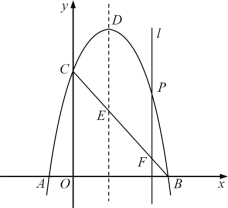
【题目】如图,二次函数y=ax2+bx+4的图象与x轴交于点A(-1,0),B(4,0),与y轴交于点C,抛物线的顶点为D,其对称轴与线段BC交于点E.垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F,动直线l在抛物线的对称轴的右侧(不含对称轴)沿x轴正方向移动到B点.
(1)求出二次函数y=ax2+bx+4和BC所在直线的表达式;
(2)在动直线l移动的过程中,试求使四边形DEFP为平行四边形的点P的坐标;
(3)连接CP,CD,在移动直线l移动的过程中,抛物线上是否存在点P,使得以点P,C,F为顶点的三角形与![]() DCE相似,如果存在,求出点P的坐标,如果不存在,请说明理由.
DCE相似,如果存在,求出点P的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,菱形ABCD中,E,F分别是对角线BD和边BC上一点,且满足∠EAF=∠ABD=![]() .
.
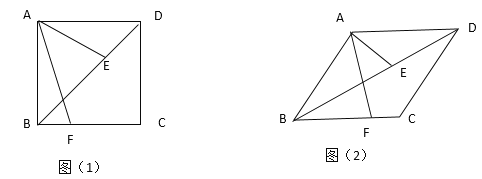
(1)如图(1),当![]() =45°时,求证:AF=
=45°时,求证:AF=![]() AE
AE
(2)如图(2),探究AF与AE的数量关系(用含![]() 的锐角三角函数表示)
的锐角三角函数表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生社团是指学生在自愿基础上结成的各种群众性文化、艺术、学术团体.不分年级、由兴趣爱好相近的同学组成,在保证学生完成学习任务和不影响学校正常教学秩序的前提下开展各种活动.某校就学生对“篮球社团、动漫社团、文学社团和摄影社团”四个社团选择意向进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整).

请根据图中信息,解答下列问题:
(1)求扇形统计图中m的值,并补全条形统计图;
(2)在“动漫社团”活动中,甲、乙、丙、丁、戊五名同学表现优秀,现决定从这五名同学中任选两名参加“中学生原创动漫大赛”,恰好选中甲、乙两位同学的概率为 .
(3)已知该校有1200名学生,请估计“文学社团”共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为奖励在家自主学习有突出表现的学生,决定购买笔记本和钢笔作为奖品.已知1本笔记本和4支钢笔共需100元,4本笔记本和6支钢笔共需190元.
(1)分别求一本笔记本和一支钢笔的售价;
(2)若学校准备购进这两种奖品共90份,并且笔记本的数量不多于钢笔数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 150 | 175 | ______ | … | ______ |
方式二的总费用(元) | 90 | 135 | ______ | … | ______ |
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车沿同一公路从A地出发前往路程为100千米的B地,乙车比甲车晚出发15分钟,行驶过程中所行驶的路程分别用y1、y2(千米)表示,它们与甲车行驶的时间x(分钟)之间的函数关系如图所示.
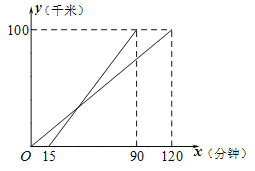
(1)分别求出y1、y2关于x的函数解析式并写出定义域;
(2)乙车行驶多长时间追上甲车?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com