【题目】(2016湖北襄阳第24题)
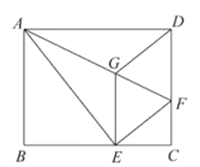
如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)探究线段EG,GF,AF之间的数量关系,并说明理由;
(3)若AG=6,EG=2![]() ,求的长.
,求的长.
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)根据已知条件易证![]() ,即可判定四边形EFDG是菱形;(2)连接ED交AF于点H,根据菱形的性质可得
,即可判定四边形EFDG是菱形;(2)连接ED交AF于点H,根据菱形的性质可得![]() 在证明RtFEH∽RtFAE,根据相似三角形的性质可得
在证明RtFEH∽RtFAE,根据相似三角形的性质可得![]() ,代入数值即可求得GF的长,再求得AD、DE的长,最后再判定RtADF∽RtDCE,即可得
,代入数值即可求得GF的长,再求得AD、DE的长,最后再判定RtADF∽RtDCE,即可得![]() ,带入数值即可得结论.
,带入数值即可得结论.
试题解析:由折叠的性质可得![]()
![]()
![]()
![]()
∴四边形EFDG是菱形.
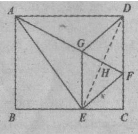
(2)连接ED交AF于点H,
∵四边形EFDG是菱形,
![]()
![]()
∴RtFEH∽RtFAE,
![]()
∵AG=6,EG=2![]() ,EG2=
,EG2=![]() ,∴(2
,∴(2![]() )2=
)2=![]()
![]()
![]()
![]()
![]()
![]() ∴RtADF∽RtDCE
∴RtADF∽RtDCE
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(﹣a+2)2﹣(a+3)(a﹣2),其中a=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不能使两个直角三角形全等的条件是( ).
A.一条直角边及其对角对应相等B.斜边和两条直角边对应相等
C.斜边和一条直角边对应相等D.两个锐角对应相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】汽车刹车后行驶的距离s(单位:米)关于行驶的时间t(单位:秒)的函数解析式是s=8t﹣2t2,汽车刹车后停下来前进的距离是______米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在纸面上有一数轴(如图),折叠纸面.
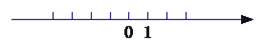
(1)若1表示的点与-1表示的点重合,则-2表示的点与数 表示的点重合;
(2)若-1表示的点与3表示的点重合,回答以下问题:
① 5表示的点与数 表示的点重合;
② 若数轴上A、B两点之间的距离为9(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆O的半径为3cm,点P是直线l上的一点,且OP=3cm,则直线l与圆O的位置关系为( )
A. 相切 B. 相交 C. 相离 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】杭州市成功申办2022年亚运会,这将推动杭州市体育事业发展,为了促进全民健身活动的发展,某社区为辖区内学校购买一批篮球和足球,已知篮球和足球的单价分别为120元和90元.
(1)根据实际需要,社区决定购买篮球和足球共100个,其中篮球购买的数量不少于40个,社区可用于购买这批篮球和足球的资金最多为10260元,请问有几种购买方案;
(2)若购买篮球
 个,学校购买这批篮球和足球的总费用为
个,学校购买这批篮球和足球的总费用为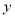 元,在(1)的条件下,求哪种方案能使
元,在(1)的条件下,求哪种方案能使 最小,并求出
最小,并求出 的最小值.
的最小值.
相关试题

