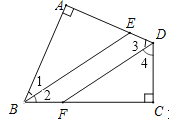
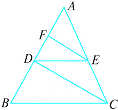
【题目】如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.
参考答案:
【答案】BE∥DF.理由见解析.
【解析】
试题分析:根据四边形的内角和定理和∠A=∠C=90°,得∠ABC+∠ADC=180°;根据角平分线定义、等角的余角相等易证明和BE与DF两条直线有关的一对同位角相等,从而证明两条直线平行.
试题解析:BE∥DF.理由如下:
∵∠A=∠C=90°(已知),
∴∠ABC+∠ADC=180°(四边形的内角和等于360°).
∵BE平分∠ABC,DF平分∠ADC,
∴∠1=∠2=![]() ∠ABC,∠3=∠4=
∠ABC,∠3=∠4=![]() ∠ADC(角平分线的定义).
∠ADC(角平分线的定义).
∴∠1+∠3=![]() (∠ABC+∠ADC)=
(∠ABC+∠ADC)=![]() ×180°=90°(等式的性质).
×180°=90°(等式的性质).
又∠1+∠AEB=90°(三角形的内角和等于180°),
∴∠3=∠AEB(同角的余角相等).
∴BE∥DF(同位角相等,两直线平行).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装原价200元,降价x%后再优惠20元,现售价为y元,y关于x的函数关系式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小正方形都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
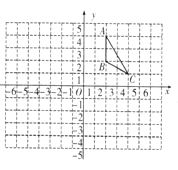
(1)作出△ABC关于
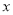 轴的对称图形△A1B1C1
轴的对称图形△A1B1C1(2)写出△ABC关于
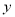 轴的对称图形△A2B2C2的顶点坐标.
轴的对称图形△A2B2C2的顶点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知DE∥BC,EF平分∠AED,EF⊥AB,CD⊥AB,求证:CD平分∠ACB .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰△ABC的周长为18 cm,BC=8 cm,若△ABC≌△A′B′C′,则△A′B′C′的腰长等于________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比,已知这本书的长为20cm,则它的宽约为( )
A.12.36 cm
B.13.6 cm
C.32.36 cm
D.7.64 cm -
科目: 来源: 题型:
查看答案和解析>>【题目】将若干只鸡放入若干笼中,若每个笼中放4只,则有一鸡无笼可放;若每个笼里放5只,则有一笼无鸡可放,问有多少只鸡,多少个笼?
相关试题

