【题目】现如今,“垃圾分类”意识已深入人心,如图是生活中的四个不同的垃圾分类投放桶,分别写着:有害垃圾、厨余垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾,小丽投放了两袋垃圾.
(1)直接写出小明投放的垃圾恰好是“厨余垃圾”的概率;
(2)求小丽投放的两袋垃圾不同类的概率.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)直接利用概率公式求出小明投放的垃圾恰好是“厨余垃圾”的概率;(2)首先利用树状图法列举出所有可能,进而利用概率公式求出答案.
解:(1)将有害垃圾、厨余垃圾、其他垃圾、可回收垃圾分别记为A,B,C,D,
∵小明投放了一袋垃圾,∴小明投放的垃圾恰好是B类:厨余垃圾的概率为:![]() ;
;
(2)画树状图如下:
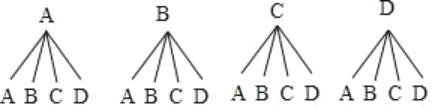
由树状图知,小丽投放的垃圾共有16种等可能结果,其中小丽投放的两袋垃圾不同类的有12种结果,所以小丽投放的两袋垃圾不同类的概率为![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为
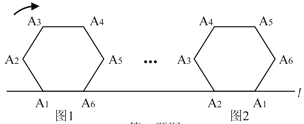
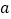 的正六边形A1A2A3A4A5A6在直线
的正六边形A1A2A3A4A5A6在直线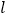 上由图1的位置按顺时针
上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的
长为( ).
A.
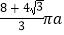 B.
B. 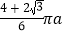 C.
C. 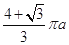 D.
D. 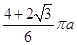
-
科目: 来源: 题型:
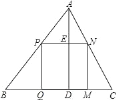
查看答案和解析>>【题目】如图,△ABC是一块锐角三角形余料,边BC=120cm,高AD=80cm,要把它加工成一个矩形零件,使矩形PQMN的一边在BC上,其余两个顶点分别在AB、AC上.设PQ=xcm,矩形PQMN的面积为ycm2,请写出y关于x的函数表达式(并注明x的取值范围)_____.
-
科目: 来源: 题型:
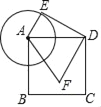
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为3,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将DE绕点D按逆时针旋转90°,得到DF,连接AF,则AF的最小值是_____.
-
科目: 来源: 题型:
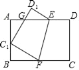
查看答案和解析>>【题目】如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的C1处,点D落在点D1处,C1D1交线段AE于点G.
(1)求证:△BC1F∽△AGC1;
(2)若C1是AB的中点,AB=6,BC=9,求AG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年12月16﹣18日,第二届互联网大会在浙江乌镇胜利举行,这说明我国互联网发展走到了世界的前列,尤其是电子商务.据市场调查,天猫超市在销售一种进价为每件40元的护眼台灯中发现:每月销售量y(件)与销售单价x(元)之间的函数关系如图所示.
(1)当销售单价定为50元时,求每月的销售件数;
(2)设每月获得利润为w(元),求每月获得利润w(元)关于销售单价x(元)的函数解析式;
(3)由于市场竞争激烈,这种护眼灯的销售单价不得高于75元,如果要每月获得的利润不低于8000元,那么每月的成本最少需要多少元?(成本=进价×销售量)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)点P在线段AB上运动的过程中,是否存在点Q,使得△BOD∽△QBM?若存在,求出点Q的坐标;若不存在,请说明理由.
(3)已知点F(0,
 ),点P在x轴上运动,试求当m为何值时以D、M、Q、F为顶点的四边形是平行四边形.
),点P在x轴上运动,试求当m为何值时以D、M、Q、F为顶点的四边形是平行四边形.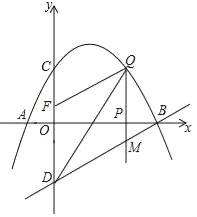
相关试题

