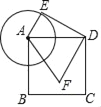
【题目】如图,已知正方形ABCD的边长为3,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将DE绕点D按逆时针旋转90°,得到DF,连接AF,则AF的最小值是_____.
参考答案:
【答案】3![]() ﹣1.
﹣1.
【解析】分析:先找出AF最大值时,点E的位置,再判断出AF最大时,点C在AF上,根据正方形的性质求出AC,从而得出AF的最大值.
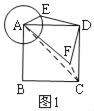
详解:如图1,连接FC,AF,
∵ED⊥DF,
∴∠EDF=∠EDA+∠ADF=90°,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ADF+∠CDF=90°,
∴∠EDA=∠CDF,
在△ADE和△CDF中,
∵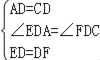 ,
,
∴△ADE≌△CDF,
∴CF=AE=1,
∴AF>AC﹣CF,即AF>AC﹣1,
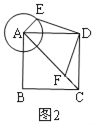
∴当F在AC上时,AF最小,如图2,
∵正方形ABCD的边长为3,
∴AC=3![]() ,
,
∴AF的最小值是3![]() ﹣1;
﹣1;
故答案为:3![]() ﹣1.
﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点A、B分别在x轴正半轴、y轴正半轴上,AO=BO,△ABO的面积为2.
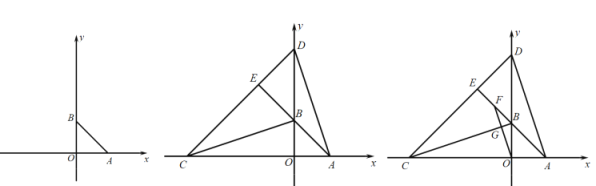
(1)求点A的坐标;
(2)点C、D分别在x轴负半轴、y轴正半轴上(D在B点上方),AD=BC,连接CD交AB延长线于E,设点E横坐标为t,△BCE的面积为S,求S与t的函数关系;
(3)在(2)的条件下,点F为BE中点,连接OF交BC于G,当∠CGO=90°时,求点D坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=ax2+bx﹣4的图象开口向上,与x轴的交点为(4,0)、(﹣2,0),则当x1=﹣1,x2=2时,对应的函数值y1和y2的大小关系为( )
A. y1>y2 B. y1=y2 C. y1<y2 D. 不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在开学期间,打算购置一批办公桌和椅子,现在同一款式的办公桌每张定价200元,椅子每张40元.国庆节期间,有两个商店决定开展促销活动,活动期间向客户提供优惠如下:
甲商店:买一张办公桌送一张椅子;
乙商店:办公桌和椅子都按定价的九折付款.
现在学校要购买20张办公桌和
 张椅子(
张椅子(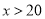 ).
).(1)用含
 的代数式表示学校分别在这两个商店购买这一批桌椅所需的费用;
的代数式表示学校分别在这两个商店购买这一批桌椅所需的费用;(2)购买椅子多少张时,两个商店的费用相等?
(3)现在学校要购买30张椅子,通过计算说明选择在哪个商店购买较为合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点
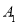 ,
,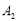 在数轴上对应的数为
在数轴上对应的数为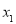 ,
,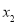 ,则称
,则称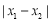 为点
为点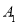 和
和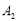 之间的距离,记作
之间的距离,记作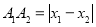 .已知数轴上两点
.已知数轴上两点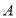 ,
,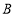 对应的数分别为
对应的数分别为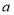 和
和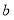 ,且满足
,且满足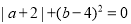 ,点
,点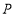 为数轴上一动点,其对应的数为
为数轴上一动点,其对应的数为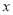 .
.(1)若点
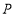 到点
到点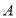 和
和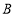 的距离相等,则点
的距离相等,则点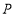 对应的数是_________.
对应的数是_________.(2)数轴上是否存在点
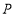 ,使
,使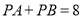 ?若存在,请求出
?若存在,请求出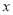 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(3)当点
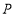 以每秒1个单位长度的速度从原点向左运动时,点
以每秒1个单位长度的速度从原点向左运动时,点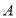 以每秒3个单位长度向左运动,点
以每秒3个单位长度向左运动,点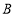 以每秒15个单位长度向左运动,若它们同时出发,几秒钟后点
以每秒15个单位长度向左运动,若它们同时出发,几秒钟后点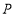 到点
到点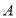 和
和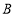 的距离相等?
的距离相等? -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且CB=5米.

(1)求钢缆CD的长度;(精确到0.1米)
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
(参考数据:tan400=0.84, sin400=0.64, cos400=
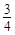 )
)
相关试题

