【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(6,4),E为AB的中点,过点D(8,0)和点E的直线分别与BC、y轴交于点F,G.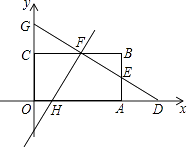
(1)求直线DE的函数关系式;
(2)函数y=mx﹣2的图象经过点F且与x轴交于点H,求出点F的坐标和m值;
(3)在(2)的条件下,求出四边形OHFG的面积.
参考答案:
【答案】
(1)
解:设直线DE的解析式为:y=kx+b,
∵顶点B的坐标为(6,4),E为AB的中点,
∴点E的坐标为:(6,2),
∵D(8,0),
∴ ![]() ,
,
解得: ![]() ,
,
∴直线DE的函数关系式为:y=﹣x+8
(2)
解:∵点F的纵坐标为4,且点F在直线DE上,
∴﹣x+8=4,
解得:x=4,
∴点F的坐标为;(4,4);
∵函数y=mx﹣2的图象经过点F,
∴4m﹣2=4,
解得:m= ![]()
(3)
解:由(2)得:直线FH的解析式为:y= ![]() x﹣2,
x﹣2,
∵ ![]() x﹣2=0,
x﹣2=0,
解得:x= ![]() ,
,
∴点H( ![]() ,0),
,0),
∵G是直线DE与y轴的交点,
∴点G(0,8),
∴OH= ![]() ,CF=4,OC=4,CG=OG﹣OC=4,
,CF=4,OC=4,CG=OG﹣OC=4,
∴S四边形OHFG=S梯形OHFC+S△CFG= ![]() ×(
×( ![]() +4)×4+
+4)×4+ ![]() ×4×4=18
×4×4=18 ![]()
【解析】(1)由顶点B的坐标为(6,4),E为AB的中点,可求得点E的坐标,又由过点D(8,0),利用待定系数法即可求得直线DE的函数关系式;(2)由(1)可求得点F的坐标,又由函数y=mx﹣2的图象经过点F,利用待定系数法即可求得m值;(3)首先可求得点H与G的坐标,即可求得CG,OC,CF,OH的长,然后由S四边形OHFG=S梯形OHFC+S△CFG , 求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】荆楚网消息,10月7日,武汉铁路局“十一”黄金周运输收官,累计发送旅客640万人,640万用科学记数法表示为( )
A.6.4×102
B.640×104
C.6.4×106
D.6.4×105 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,l1反映了甲离开A地的时间与离A地的距离的关系l2反映了乙离开A地的时间与离开A地距离之间的关系,根据图象填空:
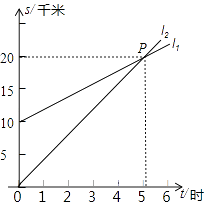
(1)当时间为0时,甲离A地千米;
(2)当时间为时,甲、乙两人离A地距离相等;
(3)图中P点的坐标是;
(4)l1对应的函数表达式是:S1=;
(5)当t=2时,甲离A地的距离是千米;
(6)当S=28时,乙离开A地的时间是时. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 等腰三角形两腰上的中线相等 B. 等腰三角形两腰上的高线相等
C. 等腰三角形的中线与高重合 D. 等腰三角形底边的中线上任一点到两腰的距离相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰三角形ABC中,∠A=100°,则∠B=________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算20192-20182的结果是( )
A. 4035 B. 4036
C. 4037 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b为有理数,且它们在数轴上的位置如图所示.
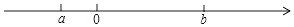
(1)在数轴上分别标出表示a,b的相反数的位置;
(2)把a,﹣a,b,﹣b按照从大到小的顺序排列并用“>”连接;
(3)若|a|=1,|b|=3,求2a﹣3b的值.
相关试题

