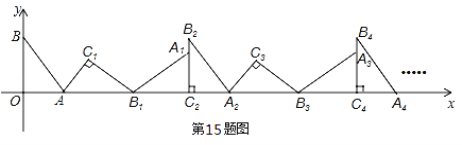
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则点B2016的坐标为( )
,0),B(0,2),则点B2016的坐标为( )
A. (4032 ,2) B. (6048,2) C. (4032,0) D. (6048,0)
参考答案:
【答案】B
【解析】首先利用勾股定理得出AB的长,进而得出三角形的周长,进而求出B2,B4的横坐标,进而得出变化规律,即可得出答案.
解:OA=![]() ,OB=2,由勾股定理,得:AB=
,OB=2,由勾股定理,得:AB=![]() ,所以,OC2=2+
,所以,OC2=2+![]() +
+![]() =6,
=6,
所以,B2(6,2),同理可得:B4(12,2),B6(18,2),…
所以,B2016的横坐标为:1008![]() 6=6048,所以,B2016(6048,2)
6=6048,所以,B2016(6048,2)
故选B.
“点睛”此题主要考查了点的坐标以及图形变化类,根据题意得出B点横坐标变化规律是解题关键.
-
科目: 来源: 题型:
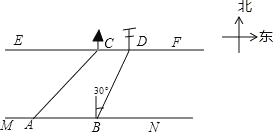
查看答案和解析>>【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为 米.(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:
销售单价x(元/kg)
120
130
…
180
每天销量y(kg)
100
95
…
70
设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=2x2先沿x轴方向向左平移2个单位,再沿y轴方向向下平移3个单位,所得抛物线的解析式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面内,两条直线l1,l2相交于点O,对于平面内任意一点M,若p,q分别是点M到直线l1,l2的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(2,1)的点共有__________个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形ABC中,∠BAC=90°,P是△ABC内一点,PA=1,PB=3,PC=
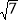 .求∠CPA的度数.
.求∠CPA的度数.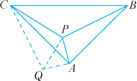
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何图形中不是中心对称图形的是( )
A. 圆 B. 平行四边形 C. 正三角形 D. 正方形
相关试题

