【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:
销售单价x(元/kg) | 120 | 130 | … | 180 |
每天销量y(kg) | 100 | 95 | … | 70 |
设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
参考答案:
【答案】(1)y=﹣0.5x+160,120≤x≤180;(2)当销售单价为180元时,销售利润最大,最大利润是7000元.
【解析】
试题分析:(1)观察由表格可知,销售单价没涨10元,就少销售5kg,即可判定y与x是一次函数关系,由待定系数法求函数解析即可;(2)设销售利润为w元,根据题意得出w与x的二次函数关系,根据二次函数的性质即可求得最大利润.
试题解析:(1)∵由表格可知:销售单价没涨10元,就少销售5kg,
∴y与x是一次函数关系,
∴y与x的函数关系式为:y=100﹣0.5(x﹣120)=﹣0.5x+160,
∵销售单价不低于120元/kg.且不高于180元/kg,
∴自变量x的取值范围为:120≤x≤180;
(2)设销售利润为w元,
则w=(x﹣80)(﹣0.5x+160)=﹣![]() x2+200x﹣12800=﹣
x2+200x﹣12800=﹣![]() (x﹣200)2+7200,
(x﹣200)2+7200,
∵a=﹣![]() <0,
<0,
∴当x<200时,y随x的增大而增大,
∴当x=180时,销售利润最大,最大利润是:w=﹣![]() (180﹣200)2+7200=7000(元),
(180﹣200)2+7200=7000(元),
答:当销售单价为180元时,销售利润最大,最大利润是7000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(﹣2,y1),B(1,y2)都在直线y=﹣2x+2上,则y1、y2的大小关系是( )
A. y1=y2B. y1<y2C. y1>y2D. y1≥y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a是不等式2x﹣1>5的解,b不是不等式2x﹣1>5的解,则下列结论正确的是( )
A. a>b B. a≥b C. a<b D. a≤b
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+2x﹣4=0的根的情况为( )
A. 没有实数根 B. 有两个相等的实数根
C. 有两个不相等的实数根 D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一根40cm的金属棒,欲将其截成x根7cm的小段和y根9cm的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )
A.
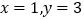 B.
B. 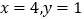 C.
C. 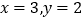 D.
D. 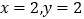
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线l与直线y=2x﹣3关于y轴对称,则直线l的解析式是( )
A. y=﹣2x+3B. y=﹣2x﹣3C. y=2x+3D. y=2x﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】两年前生产1吨甲种药品的成本是5000元.随着生产技术的进步,成本逐年下降,第2年的年下降率是第1年的年下降率的2倍,现在生产1吨甲种药品成本是2400元.为求第一年的年下降率,假设第一年的年下降率为x,则可列方程( )
A. 5000(1﹣x﹣2x)=2400 B. 5000(1﹣x)2=2400
C. 5000﹣x﹣2x=2400 D. 5000(1﹣x)(1﹣2x)=2400
相关试题

