【题目】九(1)班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”,“3”,“3”,“5”,“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖,记每次抽出两张牌点数之差为![]() ,按表格要求确定奖项.
,按表格要求确定奖项.

(1)用列表或画树状图的方法求出甲同学获得一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
参考答案:
【答案】(1)![]() (2)不一定
(2)不一定
【解析】分析:(1)画出树状图,找出符合条件的情况,求出其概率即可。
(2)根据题意分析不满足条件的情况并找出即可求是否存在不中奖的情况。
本题解析:
(1)画树状图得:
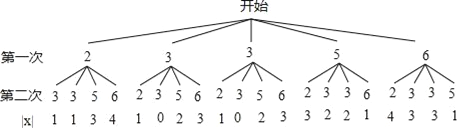
∵共有20种等可能的结果,甲同学获得一等奖的有2种情况,
∴甲同学获得一等奖的概率为: ![]() ;
;
(2)不是,当两张牌都是3时,|x|=0,不会有奖.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在等边△ABC中,点M是边BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是边BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是边BC上的任意一点(不含端点B、C),联结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个零件的形状如图,按规定∠A=90°,∠B和∠C应分别是32°和21°,检验工人量得∠BDC=148°,断定这个零件是否合格?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列已知条件,能唯一画出△ABC的是( )
A.AB=6,BC=3,AC=9B.AB=5,BC=4,∠A=30°
C.∠C=90°,AB=6D.∠A=60°,∠B=45°,AB=4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在图(1)中,猜想:∠A+∠B+∠C+∠D+∠E+∠F=______度.
请说明你猜想的理由.
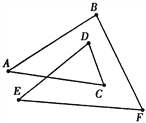
图1
如果把图1成为2环三角形,它的内角和为∠A+∠B+∠C+∠D+∠E+∠F;图2称为2环四边形,它的内角和为∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H;

图2
则2环四边形的内角和为_____________________________________________度;
2环五边形的内角和为________________________________________________度;
2环n边形的内角和为________________________________________________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若xm÷x2n+1=x,则m与n的关系是( )
A. m=2n+1 B. m=﹣2n﹣1 C. m﹣2n=2 D. m﹣2n=﹣2
相关试题

