【题目】一个零件的形状如图,按规定∠A=90°,∠B和∠C应分别是32°和21°,检验工人量得∠BDC=148°,断定这个零件是否合格?为什么?

参考答案:
【答案】不合格
【解析】试题分析:连接AD并延长至点E,由三角形外角的性质可知∠BDE=∠BAD+∠DBA、∠CDE=∠CAD+∠ACD,再结合已知条件和图形中角的关系求出∠BDC的度数,将求出的∠BDC的度数与测量的∠BDC的度数进行比较,即可得到结论.
试题解析:这个零件不合格.
理由:连接AD并延长至点E,如图所示:
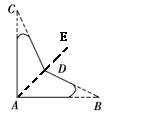
∵∠BDE=∠BAD+∠DBA,∠CDE=∠CAD+∠ACD,
∴∠BDE+∠CDE=∠BAD+∠DBA+∠CAD+∠ACD.
∵∠BDE+∠CDE=∠BAD+∠DBA+∠CAD+∠ACD,∠BDE+∠CDE=∠BDC,
∴∠BDC=∠BAD+∠DBA+∠CAD+∠ACD.
∵∠BDC=∠BAD+∠DBA+∠CAD+∠ACD,∠BAC=∠BAD+∠CAD=90°,∠DBA=32°,∠ACD=21°,
∴∠BDC=143°.
∵∠BDC=143°,但量得∠BDC=148°≠143°,
∴这个零件不合格.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|x|=4,|y|=1,且xy<0,则x﹣y= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在等边△ABC中,点M是边BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是边BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是边BC上的任意一点(不含端点B、C),联结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】九(1)班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”,“3”,“3”,“5”,“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖,记每次抽出两张牌点数之差为
 ,按表格要求确定奖项.
,按表格要求确定奖项.
(1)用列表或画树状图的方法求出甲同学获得一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列已知条件,能唯一画出△ABC的是( )
A.AB=6,BC=3,AC=9B.AB=5,BC=4,∠A=30°
C.∠C=90°,AB=6D.∠A=60°,∠B=45°,AB=4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在图(1)中,猜想:∠A+∠B+∠C+∠D+∠E+∠F=______度.
请说明你猜想的理由.
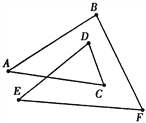
图1
如果把图1成为2环三角形,它的内角和为∠A+∠B+∠C+∠D+∠E+∠F;图2称为2环四边形,它的内角和为∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H;

图2
则2环四边形的内角和为_____________________________________________度;
2环五边形的内角和为________________________________________________度;
2环n边形的内角和为________________________________________________度.
相关试题

