【题目】一位农民带上若干千克自产的土豆进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图,结合图象回答下列问题:
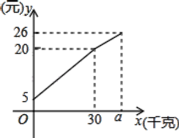
(1)农民自带的零钱是多少?
(2)求出降价前每千克的土豆价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
参考答案:
【答案】(1) 5元; (2) 0.5元; (3) 45千克;
【解析】
(1) 由图象可知,当x=0时,y=5,所以农民自带的零钱是5元.
(2) 可设降价前每千克土豆价格为k元,则可列出农民手中钱y与所售土豆千克数x之间的函数关系式,由图象知,当x=30时,y的值,从而求出这个函数式.
(3) 可设降价后农民手中钱y与所售土豆千克数x之间的函数关系式,因为当x=a时,y=26,当x=30时,y=20,依此列出方程求解即可得到答案.
解:(1) 由图象可知,当x=0时,y=5,
故农民自带的零钱是5元.
答:农民自带的零钱是5元.
(2) 设降价前每千克土豆价格为k元,
则农民手中钱y与所售土豆千克数x之间的函数关系式为:y=kx+5,
∵从图像可以看出,当x=30时,y=20,
∴20=30k+5,
解得:k=0.5,
故降价前每千克土豆是0.5元.
答:降价前每千克土豆价格为0.5元.
(3) 设降价后农民手中钱y,所售土豆千克数为x,
降价后他按每千克0.4元将剩余土豆售完,
则得到y与x之间的函数关系式为y=0.4x+b,
∵当x=30时,y=20,
∴b=8,
当x=a时,y=26,即0.4a+8=26,
解得:a=45.
答:农民一共带了45千克土豆.
-
科目: 来源: 题型:
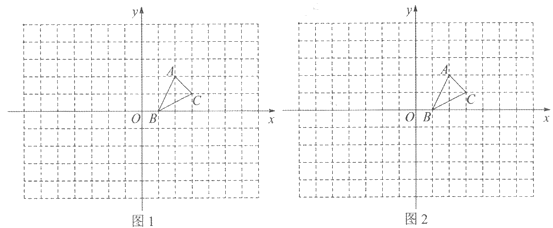
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)在图l中画出△ABC关于x轴对称的△A1B1C1;
(2)在图2中,以点O为位似中心,将△ABC放大,使放大后的△A2B2C2与△ABC的对应边的比为2:1(画出一种即可). 直接写出点A的对应点A2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,一次函数y=x+2的图象与反比例函数y=
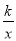 的图象交于A、B两点,且点A的坐标为(1,m).
的图象交于A、B两点,且点A的坐标为(1,m). (1)求反比例函数y=
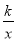 的表达式;
的表达式;(2)点C(n,1)在反比例函数y=
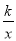 的图象上,求△AOC的面积.
的图象上,求△AOC的面积. 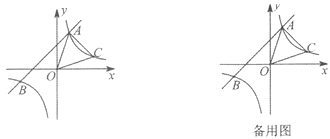
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某汽车行驶的路程S(千米)与时间t(分)的函数关系图.观察图中所提供的信息,解答下列问题:
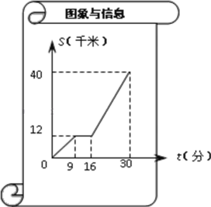
(1)汽车在前9分钟内的平均速度是______千米/分;
(2)当16≤t≤30时,求S与t的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点 P 在平面直角坐标系中按图中箭头所示方向运动,第 1 次从原点运动到点(1,1),第 2 次接着运动到点(2,0),第 3 次接着运动到点(3,2),……,按这样的运动规律,经过第2025 次运动后,动点 P 的坐标是( )
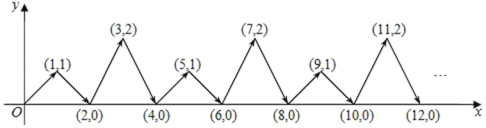
A.(2025,1)B.(2025,0)C.(2026,2)D.(2026,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是________ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一次函数 y=kx+b,当 1≤x≤4 时,3≤y≤6,则一次函数的解析式为_____.
相关试题

