【题目】探索规律,观察下面算式,解答问题.
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
…
(1)请猜想:1+3+5+7+9+…+19=________;
(2)请猜想:1+3+5+7+9+…+(2n-1)+(2n+1)+(2n+3)=________;
(3)试计算:101+103+…+197+199.
参考答案:
【答案】(1)102;(2)(n+2)2;(3)7500.
【解析】试题分析:(1)(2)观察数据可知,从1开始的连续奇数的和等于首尾两个奇数的和的一半的平方,然后计算即可得解;
(3)用从1开始到199的和减去从1开始到99的和,列式计算即可得解.
试题解析:
(1)1+3+5+7+9+…+19=(![]() )=100=10;
)=100=10;
(2)1+3+5+7+9+…+(2n1)+(2n+1)+(2n+3)=(![]() ) =(n+2) ;
) =(n+2) ;
(3)原式=(1+3+5+…+197+199)-(1+3+…+97+99)
=1002-502=7500.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程(x﹣1)(x+2)=x﹣1的解是( )
A.﹣2
B.1,﹣2
C.﹣1,1
D.﹣1,3 -
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭,小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如下表),以50 km为标准,多于50 km的记为“+”,不足50 km的记为“-”,刚好50 km的记为“0”.
第一天
第二天
第三天
第四天
第五天
第六天
第七天
路程(km)
-8
-11
-14
0
-16
+41
+8
(1)请求出这七天中平均每天行驶多少千米?
(2)若每天行驶100 km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?
-
科目: 来源: 题型:
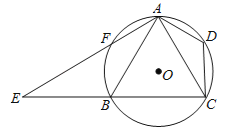
查看答案和解析>>【题目】如图,已知四边形ABCD内接于⊙O,A是
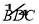 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且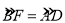 .
.(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】满足下列条件的△ABC不是直角三角形的是( )
A. BC=1,AC=2,AB=
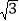 ; B. BC:AC:AB=3:4:5
; B. BC:AC:AB=3:4:5C. ∠A+∠B=∠C D. ∠A:∠B:∠C=3:4:5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣(x+h)2,当x<﹣3时,y随x的增大而增大,当x>﹣3时,y随x的增大而减小,当x=0时,y的值为( )
A. ﹣1B. ﹣9C. 1D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简a﹣(b﹣c)正确的是( )
A. a﹣b+c B. a﹣b﹣c C. a+b﹣c D. a+b+c
相关试题

