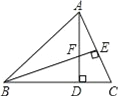
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1.2,AC=3时,求BF的长.
参考答案:
【答案】(1)证明见解析;(2)BF=2.5.
【解析】试题分析:(1)由AD⊥BC,BE⊥AC,∠BDF=∠ADC=∠BEC=90°,从而得到∠DBF=∠DAC, 问题得证;
(2)由tan∠ABD=1.2,∠ADB=90°,可得AD与BD的比值,再由相似三角形的对应边的比相等,由(1)中的两三角形相似即可求得BF的值.
试题解析:(1)∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=∠BEC=90°,
∴∠C+∠DBF=90°,∠C+∠DAC=90°,
∴∠DBF=∠DAC,
∴△ACD∽△BFD.
(2)∵tan∠ABD=1,∠ADB=90°
∴![]() =1.2,
=1.2,
∵△ACD∽△BFD,
∴![]() =1.2,
=1.2,
∵AC=3
∴BF=2.5.
-
科目: 来源: 题型:
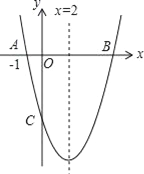
查看答案和解析>>【题目】如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(﹣1,0)
(1)求抛物线的解析式;
(2)直接写出B、C两点的坐标;
(3)求过O,B,C三点的圆的面积.(结果用含π的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,过点A(﹣
 ,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根
,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根(1)求线段BC的长度;
(2)试问:直线AC与直线AB是否垂直?请说明理由;
(3)若点D在直线AC上,且DB=DC,求点D的坐标;
(4)在(3)的条件下,直线BD上是否存在点P,使以A、B、P三点为顶点的三角形是等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=-1是方程2x+ax=0的解,则a=。
-
科目: 来源: 题型:
查看答案和解析>>【题目】要调查下列问题,你认为哪些适合抽样调查( )
①市场上某种食品的某种添加剂的含量是否符合国家标准
②检测某地区空气质量
③调查全市中学生一天的学习时间.
A. ①② B. ①③ C. ②③ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据有40个,把它分成六组,第一组到第四组的频数分别是5,10,6,7,第五组的频率是0.2,故第六组的频数是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形的两边长分别为3和6,则第三边长可能是( )
A.6B.3C.2D.10
相关试题

