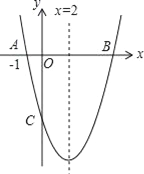
【题目】如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(﹣1,0)
(1)求抛物线的解析式;
(2)直接写出B、C两点的坐标;
(3)求过O,B,C三点的圆的面积.(结果用含π的代数式表示)
参考答案:
【答案】(1)y=x2﹣4x﹣5;(2)B(5,0),C(0,﹣5);(3)![]() π.
π.
【解析】试题分析:(1)利用对称轴方程可求得b,把点A的坐标代入可求得c,可求得抛物线的解析式;(2)根据A、B关于对称轴对称可求得点B的坐标,利用抛物线的解析式可求得B点坐标;(3)根据B、C坐标可求得BC长度,由条件可知BC为过O、B、C三点的圆的直径,可求得圆的面积.
试题解析:(1)由A(﹣1,0),对称轴为x=2,可得 ,解得
,解得![]() ,
,
∴抛物线解析式为y=x2﹣4x﹣5;
(2)由A点坐标为(﹣1,0),且对称轴方程为x=2,可知AB=6,
∴OB=5,
∴B点坐标为(5,0),
∵y=x2﹣4x﹣5,
∴C点坐标为(0,﹣5);
(3)如图,连接BC,则△OBC是直角三角形,

∴过O、B、C三点的圆的直径是线段BC的长度,
在Rt△OBC中,OB=OC=5,
∴BC=5![]() ,
,
∴圆的半径为![]() ,
,
∴圆的面积为π(![]() )2=
)2=![]() π.
π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下问题,不适合用普查的是( )
A. 了解一批灯泡的使用寿命 B. 中学生参加高考时的体检
C. 了解全校学生的课外读书时间 D. 旅客上飞机前的安检
-
科目: 来源: 题型:
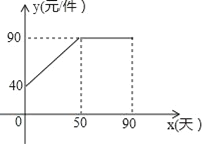
查看答案和解析>>【题目】九年级某班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天)
1
30
60
90
每天销售量p(件)
198
140
80
20
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个平面截下列几何体,截面可能是三角形的是( )
①正方体②球体③圆柱④圆锥
A.①
B.①②
C.①④
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,过点A(﹣
 ,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根
,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根(1)求线段BC的长度;
(2)试问:直线AC与直线AB是否垂直?请说明理由;
(3)若点D在直线AC上,且DB=DC,求点D的坐标;
(4)在(3)的条件下,直线BD上是否存在点P,使以A、B、P三点为顶点的三角形是等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=-1是方程2x+ax=0的解,则a=。
-
科目: 来源: 题型:
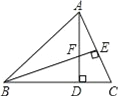
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1.2,AC=3时,求BF的长.
相关试题

