【题目】有一块长为80厘米,宽为60厘米的长方形木块,现要锯成同样大小的正方形(正方形的边长为整数),且不能有剩余,则长方形最少可以锯成几块正方形?
参考答案:
【答案】最少可以锯成12块正方形.
【解析】试题分析:由题意,正方形边长为整数且能整除长方形木块的长与宽,所以正方形的边长应为长方形木块长与宽的公因式,而所求正方形要求尽量大,故应为最大公因式,然后根据边长计算个数即可.
试题解析:80与60的最大公因数是20,
所以块数最少的正方形的边长为20厘米.
80÷20=4,60÷20=3;
4×3=12(块).
答:长方形最少可以锯成12块正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明的外婆从家乡带来一篮苹果,小明数了数,发现每次拿出4个、每次拿出5个或每次拿出6个,都恰好拿完,又知道苹果的总数超过100个,但又不足150个,试问这篮苹果共多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:

①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一条东西向道路与一条南北向道路的交汇处有一座雕像,甲车位于雕像东方5 km处,乙车位于雕像北方7 km处.若甲、乙两车以相同的速度向雕像方向同时驶去,当甲车到雕像西方1 km处时,乙车在()
A. 雕像北方1 km处 B. 雕像北方3 km处 C. 雕像南方1 km处 D. 雕像北方3 km处
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(m+2)x2+mx+m2-4=0有一个根是0,则m= ______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上点,连接EF.
(1)图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF,求AE的长;
(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图③,若FE的延长线与BC的延长线交于点N,CN=1,CE=
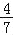 ,求
,求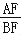 的值.
的值.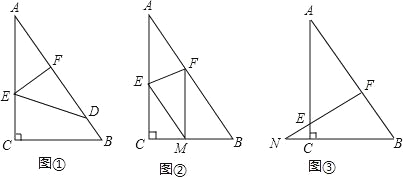
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题①等弧所对的圆心角相等;②相等的圆心角所对的弧相等;③圆中两条平行弦所夹的弧相等;④三点确定一个圆;⑤在同圆或等圆中,相等的弦所对的弧相等.其中正确的是__(填序号).
相关试题

