【题目】如图,在△ABC中,AD,BE分别为边BC,AC上的高线,D,E为垂足,M为AB的中点,N为DE的中点.求证:
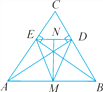
(1)△MDE是等腰三角形.
(2)MN⊥DE.
参考答案:
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:
(1)AD,BE分别为边BC,AC上的高线,D,E为垂足,可得△ADB、△BEA是直角三角形,由M是AB边的中点,可得DM=EM=![]() AB,就可得△MDE是等腰三角形;
AB,就可得△MDE是等腰三角形;
(2)由△MDE是等腰三角形,N是底边DE的中点,可得MN⊥DE.
试题解析:
(1)∵AD,BE分别为边BC,AC上的高线,
∴△ABD,△ABE均为Rt△.
∵M是Rt△ABD斜边AB的中点,
∴MD=![]() AB.
AB.
同理,ME=![]() AB.
AB.
∴ME=MD.
∴△MDE是等腰三角形.
(2)∵在△MDE中,ME=MD,N是DE的中点,
∴MN⊥DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售甲、乙两种品牌的智能手机,甲品牌手机的进价是4000元/部,售价为4300元/部,乙品牌的售价进价是2500元/部,售价为3000元/部,该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元,该商场计划购进甲、乙两种手机各多少部?(毛利润=(售价﹣进价)×销售量)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段,哪一组不能构成三角形( )
A. 3,3,3 B. 3,4,5 C. 5,6,10 D. 4,5,9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)判断四边形AOCD是否为菱形?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算a2+4a2的结果是( )
A. 4a2B. 5a2C. 4a4D. 5a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(a-4,2b+2),当a,b分别满足什么条件时:
(1)点P在第一象限?
(2)点P在第四象限?
(3)点P在x轴上?
(4)点P在y轴上?
(5)点P在x轴下方?
(6)点P在y轴左侧?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
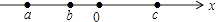
A.a>b
B.|a﹣c|=a﹣c
C.﹣a<﹣b<c
D.|b+c|=b+c
相关试题

