【题目】已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根x1,x2,请用配方法探索有实数根的条件,并推导出求根公式,证明x1x2=![]() .
.
参考答案:
【答案】证明见解析.
【解析】由a不为0,在方程两边同时除以a,把二次项系数化为1,然后把常数项移项到方程右边,两边都加上一次项系数一半的平方即(![]() )2,左边变为完全平方式,右边大于等于0时,开方即可得到求根公式;由求根公式求出的两个根相乘,化简后即可得证.
)2,左边变为完全平方式,右边大于等于0时,开方即可得到求根公式;由求根公式求出的两个根相乘,化简后即可得证.
∵ax2+bx+c=0(a≠0),
∴x2+![]() x=﹣
x=﹣![]() ,
,
∴x2+![]() x+(
x+(![]() )2=﹣
)2=﹣![]() +(
+(![]() )2,
)2,
即(x+![]() )2=
)2=![]() ,
,
∵4a2>0,
∴当b2﹣4ac≥0时,方程有实数根,
∴x+![]() =±
=±![]() ,
,
∴当b2﹣4ac>0时,x1=![]() ,x2=
,x2=![]() ;
;
当b2﹣4ac=0时,x1=x2=﹣![]() ;
;
∴x1x2=![]()
![]()
=![]()
=![]()
=![]()
=![]() ,
,
或x1x2=(﹣![]() )2=
)2=![]() =
=![]() =
=![]() ,
,
∴x1x2=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
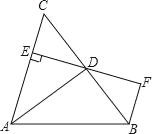
A. ①②③④ B. ①②④ C. ①②③ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a,b,c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有_________处。(填数字)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= ______ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图点P为△ABC的外角∠BCD的平分线上一点,PA=PB.
(1)如图1,求证:∠PAC=∠PBC;
(2)如图2,作PE⊥BC于E,若AC=5,BC=11,则
 = ;
= ;(3)如图3,若M、N分别是边AC、BC上的点,且∠MPN=
 ∠APB,则线段AM、MN、BN 之间有何数量关系,并说明理由.
∠APB,则线段AM、MN、BN 之间有何数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
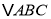 中,
中,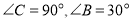 ,以
,以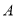 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交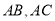 于点
于点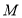 和
和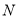 ,再分别以点
,再分别以点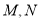 为圆心,大于
为圆心,大于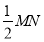 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点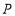 ,连接
,连接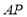 并延长交
并延长交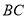 于点
于点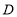 ,则下列说法①
,则下列说法①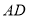 平分
平分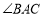 ;②
;②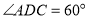 ;③点
;③点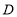 在
在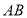 的垂直平分线上;④连接
的垂直平分线上;④连接 ,则
,则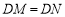 ,其中正确的是__________.(填序号)
,其中正确的是__________.(填序号)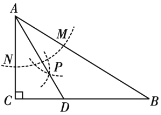
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且
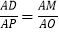 .
.(1)求证:PD是⊙O的切线;
(2)若AD=12,AM=MC,求
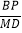 的值.
的值.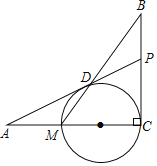
相关试题

