【题目】已知:如图,△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题: 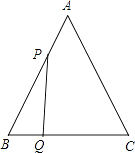
(1)经过 ![]() 秒时,求△PBQ的面积;
秒时,求△PBQ的面积;
(2)当t为何值时,△PBQ是直角三角形?
(3)是否存在某一时刻t,使四边形APQC的面积是△ABC面积的三分之二?如果存在,求出t的值;不存在请说明理由.
参考答案:
【答案】
(1)解:经过 ![]() 秒时,AP=
秒时,AP= ![]() cm,BQ=
cm,BQ= ![]() cm,
cm,
∵△ABC是边长为3cm的等边三角形,
∴AB=BC=3cm,∠B=60°,
∴BP=3﹣ ![]() =
= ![]() cm,
cm,
∴△PBQ的面积= ![]() BPBQsin∠B=
BPBQsin∠B= ![]() ×
× ![]() ×
× ![]() ×
× ![]() =
= ![]()
(2)解:设经过t秒△PBQ是直角三角形,
则AP=tcm,BQ=tcm,
△ABC中,AB=BC=3cm,∠B=60°,
∴BP=(3﹣t)cm,
△PBQ中,BP=(3﹣t)cm,BQ=tcm,若△PBQ是直角三角形,则∠BQP=90°或∠BPQ=90°,
当∠BQP=90°时,BQ= ![]() BP,
BP,
即t= ![]() (3﹣t),t=1(秒),
(3﹣t),t=1(秒),
当∠BPQ=90°时,BP= ![]() BQ,
BQ,
3﹣t= ![]() t,t=2(秒),
t,t=2(秒),
答:当t=1秒或t=2秒时,△PBQ是直角三角形
(3)解:过P作PM⊥BC于M,
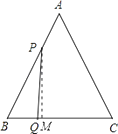
△BPM中,sin∠B= ![]() ,
,
∴PM=PBsin∠B= ![]() (3﹣t),
(3﹣t),
∴S△PBQ= ![]() BQPM=
BQPM= ![]() t
t ![]() (3﹣t),
(3﹣t),
∴y=S△ABC﹣S△PBQ= ![]() ×32×
×32× ![]() ﹣
﹣ ![]() ×t×
×t× ![]() (3﹣t)
(3﹣t)
= ![]() t2﹣
t2﹣ ![]() t+
t+ ![]() ,
,
∴y与t的关系式为y= ![]() t2﹣
t2﹣ ![]() t+
t+ ![]() ,
,
假设存在某一时刻t,使得四边形APQC的面积是△ABC面积的 ![]() ,
,
则S四边形APQC= ![]() S△ABC,
S△ABC,
∴ ![]() t2﹣
t2﹣ ![]() t+
t+ ![]() =
= ![]() ×
× ![]() ×32×
×32× ![]() ,
,
∴t2﹣3t+3=0,
∵(﹣3)2﹣4×1×3<0,
∴方程无解,
∴无论t取何值,四边形APQC的面积都不可能是△ABC面积的 ![]() .
.
【解析】(1)根据路程=速度×时间,求出BQ,AP的值,再求出BP的值,然后利用三角形的面积公式进行解答即可;(2)①∠BPQ=90°;②∠BQP=90°.然后在直角三角形BQP中根据BP,BQ的表达式和∠B的度数进行求解即可.(3)本题可先用△ABC的面积﹣△PBQ的面积表示出四边形APQC的面积,即可得出y,t的函数关系式,然后另y等于三角形ABC面积的三分之二,可得出一个关于t的方程,如果方程无解则说明不存在这样的t值,如果方程有解,那么求出的t值即可
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形ABCD的边长为6,点E,F分别在边AD,边AB的延长线上,且DE=BF.
(1)如图1,连接CE,CF,EF,请判断△CEF的形状;
(2)如图2,连接EF交BD于M,当DE=2时,求AM的长;
(3)如图3,点G,H分别在边AB,边CD上,且GH=3
 ,当EF与GH的夹角为45°时,求DE的长.
,当EF与GH的夹角为45°时,求DE的长.
-
科目: 来源: 题型:
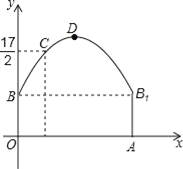
查看答案和解析>>【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣
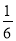 x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为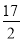 m.
m.(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料: 如图1,在数轴上A点衰示的数为a,B点表示的数为b,则点A到点B的距离记为AB.线段AB的长可以用右边的数减去左边的数表示,即AB﹣b﹣a.
请用上面的知识解答下面的问题:
如图2,一个点从数轴上的原点开始,先向左移动1cm到达A点,再向左移动2cm到达B点,然后向右移动7cm到达C点,用1个单位长度表示1cm.
(1)请你在数轴上表示出A.B.C三点的位置:
(2)点C到点人的距离CA=cm;若数轴上有一点D,且AD=4,则点D表示的数为;
(3)若将点A向右移动xcm,则移动后的点表示的数为;(用代数式表示)
(4)若点B以每秒2cm的速度向左移动,同时A.C点分别以每秒1cm、4cm的速度向右移动.设移动时间为t秒, 试探索:CA﹣AB的值是否会随着t的变化而改变?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】请将下列各数填入相应的集合内: ﹣
 ,1.010010001,0,π,
,1.010010001,0,π, 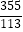 ,﹣2.626626662…(每2个2之间依次多1个6),﹣0.1
,﹣2.626626662…(每2个2之间依次多1个6),﹣0.1 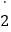 .
.
正数集合:{ };
负数集合:{ };
有理数集合:{ };
无理数集合:{ }. -
科目: 来源: 题型:
查看答案和解析>>【题目】在圆内接四边形ABCD中,若∠A∶∠B∶∠C=1∶2∶5,则∠B的度数是( )
A. 30°B. 45°C. 60°D. 120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果菱形的两条对角线的长分别为6cm和8cm,则此菱形的边长是 cm,面积是 cm2.
相关试题

